Биофизика системы кровообращения гидродинамика гемодинамика Гидродинамика

Биофизика системы кровообращения

гидродинамика гемодинамика Гидродинамика – раздел механики сплошных сред, в котором изучается движение несжимаемых жидкостей (плотность постоянна) и взаимодействие этих жидкостей с твердыми телами. Гемодинамика изучает движение крови по сосудам, возникающее вследствие разности гидростатического давления в различных участках сосудистой системы

Основные гемодинамические показатели 1. Скорость кровотока 2. Кровяное давление 3. Общее периферическое сопротивление сосудов (ОПСС)

Скорость тока жидкости Линейная: расстояние, пройденное за единицу времени Объемная: объем жидкости, прошедший за единицу времени через единицу поперечного сечения S

Для каждой точки пространства нужно знать вектор скоростив каждый момент времени (поле скоростей) Линии тока- линии, касательные к которым совпадают с направлением вектора скорости течения жидкости v При стационарном течении любая частица жидкости проходит через данную точку с одной и той же скоростью: поле скоростей и линии поля не меняются

Трубка тока Часть жидкости между линиями тока S 2 S 1 ! Частицы жидкости при движении не пересекают стенок трубки !

Условие неразрывности струи Закон сохранения массы

Теорема о неразрывности струи Возьмем очень тонкую трубку тока – скорость всех частиц в ней будем считать постоянной и перпендикулярной сечению S За единицу времени

Теорема о неразрывности струи За единицу времени через сечения S 1 и S 2 протекают равные массы жидкости S 2 S 1

Выводы В разветвленной трубке объемная скорость потока одинакова во всех суммарных поперечных сечениях

10 см/с 5 см/с 2 см 2 4 см 2 При заданной объемной скорости жидкости, изменение сечения приводит к пропорциональному изменению линейной скорости

Условие неразрывности струи выполняется в гемодинамике: в любом сечении сердечнососудистой системы объемная скорость кровотока одинакова (около 5 л/мин в покое) Площадь суммарного просвета всех капилляров в 700 – 800 раз больше поперечного сечения аорты. В первом приближении скорость движения по капиллярам в 700 раз меньше, чем в аорте (1 мм/с)

Задача 1 Наблюдая под микроскопом движение эритроцитов в капилляре, можно измерить скорость течения крови (vк= 0, 5 мм/с). Средняя скорость крови в аорте составляет 40 см/с. Определите, во сколько раз сумма поперечных сечений капилляров больше сечения аорты.

Решение

Течение вязких жидкостей

Неидеальная жидкость, силы внутреннего трения Будем равномерно двигать верхнюю пластину v F v 0 Fтр d z V=0 Сила F уравновешивается противоположно направленной силой Fтр

Коэффициент внутреннего трения (вязкость) Найдено, что Площадь пластин Эта формула определяет силу трения между соприкасающимися слоями жидкости

скорость меняется в разных слоях по линейному закону Вязкость Скорость сдвига Формула определяет модуль силы трения

Единицей вязкости в системе СИ является вязкость, при которой градиент скорости 1 м/с на 1 см приводит к возникновению силы трения 1 дин на 1 см 2 касающихся слоев: 1 Па∙с = 10 Пуаз Вязкость воды = 1 м. Па ∙с = 1 с. П Вязкость крови в норме около 5 с. П (5 м. Па ∙с в 5 раз больше вязкости воды)

Коэффициент вязкости зависит от температуры: у жидкостей сильно уменьшается с повышением температуры (при нагреве воды от 0 до 20 градусов вязкость уменьшается почти в два раза)

По вязким свойствам жидкости делятся на 1. Ньютоновские: η зависит от природы жидкости и температуры; 2. Неньютоновские: η зависит, кроме того, от условий течения жидкости (в частности, от скорости сдвига)

Кровь – неньютоновская жидкость Пример неньютоновской жидкости – суспензии; Кровь — суспензия эритроцитов в физиологическом растворе, Дополнительная сложность — эритроциты способны к агрегации, условия образования агрегатов различны при разных скоростях течения Структура крови различна в разных сосудах

Крупные сосуды (аорта, артерии) dс>>dэр; dс>dагр Образуются конгломераты, вязкость невелика (5 м. Па∙с) Мелкие сосуды (артериолы) dс~(5 -20)dэр; dс~dагр Вязкость велика – 800 м. Па∙с. В сосудах тоньше 0, 5 мм вязкость уменьшается пропорционально уменьшению диаметра (эффект Фареуса. Линдквиста)

Капилляры dс

Характер течения жидкости

Ламинарное и турбулентное течение Жидкость можно разделить на несмешивающиеся слои – ламинарное ( «слоистое» ) течение; стационарно Скорость частиц меняется беспорядочно, жидкость перемешивается, течение турбулентное

Работа сердца зависит от Q При ламинарном течении При турбулентном течении

Осборн Рейнольдс: Характер течения зависит от безразмерной величины: Коэффициент вязкости Размер сечения Плотность жидкости До Re* течение ламинарное, после турбулентное

Для круглой трубы диаметра D Уже при Re = 400 возникают локальные завихрения в изгибах и разветвлениях артерий Кинематическая вязкость Динамическая вязкость Число Рейнольдса используют для сравнения характера течения

Пример клинической значимости гидродинамических факторов Атеросклероз Поток в области ответвлений почечных артерий от абдоминальной аорты Sabbah et al. 1984. Flow separation in the renal arteries. Arteriosclerosis, 4: 28 -33.

Задача 2 Рассчитайте число Рейнольдса для артериального кровотока, приняв кровь как ньютоновскую жидкость. Динамическая вязкость крови 5000 мк. Па∙с, диаметр аорты 2, 5 см, плотность 1, 06 г/мл. Скорость движения крови 40 см/с. Каков характер течения, если Re*=2000?

Решение

Кровяное давление и общее периферическое сопротивление сосудов Закон Пуазейля

Течение жидкости в круглой трубе При движении жидкости в круглой трубе скорость равна нулю у стенок и максимальна по оси трубы. Течение стационарное и ламинарное. Найдем v(r).

Выделим внутри трубы коаксиальный цилиндр Fтр r p 2 p 1 l

При стационарном течении сумма всех внешних сил, приложенных к любому объему жидкости равна нулю. Внутренние силы : на основание цилиндра в направлении движения жидкости действуют силы давления

На боковую поверхность трубы действует сила трения

Условие стационарности Так как скорость убывает с расстоянием от оси трубы

Разделим переменные После интегрирования

На стенках трубы скорость должна быть равна нулю v = 0 при r = R

На оси трубы r = 0 Ламинарное течение: профиль параболический Турбулентное течение

Вычислим поток Q Объем жидкости, протекающий через поперечное сечение трубы за единицу времени Объем, проходящий через кольцо за 1 секунду r dr R скорость Площадь кольца

При ламинарном течении среднее по сечению значение скорости равно половине скорости на оси трубы.

Формула Пуазейля Подставим значение для v 0 Объемная скорость тока жидкости

Закон Пуазейля применим к ламинарному потоку гомогенных ньютоновских жидкостей в прямых жестких цилиндрических трубках.

Если кровь течет по нескольким сосудам одинакового калибра (n), включенным параллельно,

Решим уравнение Пуазейля относительно давления w ОПСС сильно зависит от радиуса сосуда Гемодинамическое сопротивление (общее периферическое сопротивление сосудов, ОПСС) Разность давлений (кровяное давление) зависит от объемной скорости кровотока (массы крови и сократительной деятельности сердца) и ОПСС (в основном, радиус сосуда) Регуляция АД связана с изменением просвета сосудов

Анализ уравнения Пуазейля w Сравним с законом Ома: U = RI Аналогия с законом Ома позволяет моделировать кровообращение при помощи электрических цепей

Резистивная модель

Гемодинамическое сопротивление При последовательном включении сосудов При параллельном включении сосудов если при разветвлении получаются сосуды одного диаметра

Суммарное ОПСС W = 140 Па∙с /мл На артериовенозные аностомозы и сосуды-сфинктеры 2%

wаорты

Процентное соотношение гидродинамического сопротивления емкости площади поверхности в различных отделах сосудистого русла

Задача 4 Средняя линейная скорость кровотока в артерии диаметром 1 см равна 5 мм/с. Вычислите объемную скорость кровотока в этом сосуде.

Задача 5 Во сколько раз гидравлическое сопротивление участка артерии больше гидравлического сопротивления такого же участка аорты, если ее радиус в 10 раз больше радиуса артерии, а вязкость крови в артерии составляет 0, 8 вязкости крови в аорте?

Решение

Задача 6 Определите максимальное количество крови, которое может пройти через аорту в 1 секунду, чтобы течение сохранилось ламинарным. Диаметр аорты 2, 5 см, вязкость крови 5 м. Па∙с. Re* = 1260.

Движение тел в жидкостях

Формула Стокса При малых Re Скорость движения тела относительно жидкости Характерный размер тела Сила сопротивления движению шарика в жидкостях при небольших скоростях

Равномерное падение шарика в вязкой жидкости Сила тяжести

Задача 7 Определите, в течение какого времени в комнате высотой h = 3 м полностью выпадет пыль (частицы шарообразные диаметром 1 мкм, плотность вещества 2, 5 г/см 3, плотность воздуха 1, 29 кг/м 3, вязкость воздуха 18, 1 мк. Па∙с).

Решение

Эффект Допплера

Допплерография

УЗДГ — ультразвуковая допплерография — это современный метод обследования кровеносных сосудов головного мозга, верхних и нижних конечностей. Допплерография позволяет определить нарушения кровотока связанные со спазмом, стенозом, тромбозом сосудов. С помощью УЗДГ можно выявить наличие атеросклеротических бляшек в артериях, определить уровень поражения сосуда, степень стеноза, оценить эффективность коллатерального кровотока.

изменение частоты принимаемых волн при относительном движении источника и приёмника (наблюдателя).

Волны от источника в покое Наблюдатели в покое видят волны отовсюду с одной и той же частотой и длиной волны

Эффект Допплера Источник движется влево; Наблюдатель слева (приближающийся источник) видит увеличенную частоту (фиолетовый сдвиг) Наблюдатель справа (удаляющийся источник) видит красный сдвиг

Случай с Р. Вудом Истинная частота источника Частота, которую видит наблюдатель Угол между скоростью источника и направлением распространения волны Скорость наблюдателя

Считаем угол равным нулю (cos =1) Длина волны, соответствующая красному цвету, равна примерно 650 нм. Зеленому цвету соответствует длина волны около 550 нм. Таким образом, изменение длины волны вследствие эффекта Доплера должна бы составлять 550650 = 0, 85 Это означает, что частота электромагнитных колебаний, попадающих в глаз автомобилиста, должна вследствие взаимного сближения его и источника света возрасти в 1

Гидро- и гемодинамика

Решить задачи.

Скорость течения жидкости в некотором сечении горизонтальной трубы равна 10 см/с. Найти скорость течения жидкости в сечении, радиус которого вдвое меньше.

Скорость течения воды во всех сечениях наклонной трубки одинакова. Найти разность давлений P в двух точках, высоты которых над уровнем Земли отличаются на h=1,5 м. Плотность воды 1000 кг/м³.

Рассчитать коэффициент вязкости жидкости, если при соприкосновении двух слоев жидкости с площадью 0,01 м², сила взаимодействия между слоями равна 0,002 Н. Скорость сдвига с^-1.

Какова площадь соприкосновения двух слоев жидкости, если при 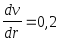с^-1 сила взаимодействия между слоями равна 610^-5 Н. Коэффициент вязкости жидкости =10^-3 Пас.

Определить весовое давление крови в артериях голени человека в положении стоя, если расстояние от сердца до заданной точки равно 1 м. Плотность крови 1050 кг/м³, ускорение свободного падения принять равным 10 м/с².

Определить среднюю скорость течения воды по трубе, изображенной на рисунке, если 1 трубка дает показания 1,5 кПа, а вторая — 14 кПа. Плотность воды 1000 кг/м³.

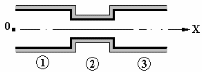
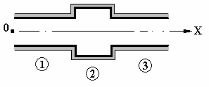
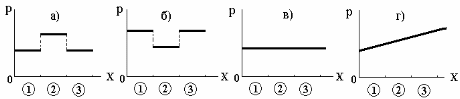
В потоке жидкости помещены две манометрические трубки 1 и 2 ( см. рисунок к задаче 7). Первая трубка дает показания 1.2 кПа, вторая — 15 кПа. Какова величина динамического давления?

Вычислить статическое давление в движущейся воде, если полное давление в потоке 10,5 кПа, скорость течения воды 1 м/с, плотность воды 1000 кг/м³.

Две манометрические трубки 1 и 2 помещены в поток жидкости так, как показано на рисунках. Выберите правильные соотношения между высотами жидкости в трубках. Выбор обоснуйте.

Жидкость течет по трубе сечением S, р₁ и р₂ — статические давления по обе стороны выбранного объема жидкости длиной l . В каком случае направление вектора скорости выбрано верно? Ответ обоснуйте.

На рисунках цифрами 1, 2, 3 обозначены участки трубы переменного сечения. Укажите график, выражающий зависимости статического давления от расстояния вдоль оси трубы

Найти скорость течения ртути через трубку диаметром 8 мм, при которой поток станет турбулентным. Плотность ртути =13,610³ кг/м³, =1,5510^-3Пас, Re=2000. За характерный размер принять диаметр.

На рисунке цифрами 1,2 , 3 обозначены участки трубы переменного сечения. Указать график зависимости динамического давления от расстояния вдоль осевой линии трубы. Выбор объяснить.

Вычислить число Re для трубы радиусом 0.179 м, если скорость течения воды 1 см/с, вязкость воды 0,00179 Пас, плотность 1000 кг/м³. Характерным линейным размером трубы считать диаметр.

Какое количество крови протекает через поперечное сечение аорты за 1 сек, если диаметр аорты 1 см, а скорость течения крови в аорте 0,5 м/с?

Какова величина гидравлического сопротивления участка трубы длиной 6,28м, если радиус трубы 10 см и по трубе течет жидкость с коэффициентом вязкости 0,001 Пас?

Как быстро ртуть может пройти через трубку диаметром 8 мм, чтобы поток не стал турбулентным? Плотность ртути =13,610³ кг/м³, =1,5510^-3Пас. Число Рейнольдса принять равным 2000.

Определить расход жидкости, протекающей по трубе радиусом 5 см, длиной 50 см, если разность давлений на концах трубы P=210^-3 Па. Коэффициент вязкости жидкости — 4 мПас.

Измерение давления крови проводят на плечевой артерии. Эта артерия имеет радиус примерно 0,005 метра, а расстояние от дуги аорты до точки измерения приблизительно равно 0,3 м. Расход крови в плечевой артерии примерно равен 10^-5м³/с. Вычислить P между аортой и точкой измерения. Вязкость крови 5мПас.

Определить максимальное количество крови (расход), которое может пройти через аорту за 1 секунду, чтобы течение сохранилось ламинарным. Диаметр аорты 2 см, вязкость крови 5 мПас, плотность крови 1050 кг/м³, Re=2000.

Укажите величину критической скорости течения воды по трубе диаметром 10 см, если плотность воды 1000 кг/м³, вязкость 0,001 Пас. Число Рейнольдса, при котором ламинарное течение становится турбулентным равно 2000.

Определить скорость пульсовой волны в сосуде, если модель упругости E=37,810⁴Па, толщина стенки сосуда h=0,05 см, диаметр сосуда 0,5 см. Плотность крови 1050 кг/м³.

Скорость пульсовой волны в артериях составляет 8 м/с. Чему равен модуль упругости этих сосудов, если известно, что отношение радиуса просвета к толщине стенки сосуда равно 6. А плотность крови — 1,05 г/см³?

Считая, что в среднем сердце совершает одно сокращение в секунду, найти работу сердца за сутки.

Рассчитать работу которую совершает сердце человека за 50 лет жизни, считая, что сердце совершает одно сокращение в секунду.

Рассчитать работу сердца при активной мышечной деятельности, если ударный объем крови 10^-4 м³, плотность крови 1050 кг/м³, скорость кровотока 1 м/с, среднее давление P=15 кПа.

Задания для самостоятельной работы. 1. Допустим, что в двух кровеносных сосудах градиент давления одинаков

1. Допустим, что в двух кровеносных сосудах градиент давления одинаков, а поток крови (объемный расход) во втором сосуде на 80 % меньше, чем в первом. Найти отношение их диаметров.

Ответ: .

2. Оценить минимально допустимое АД у жирафа, ниже которого кровоснабжение мозга становится невозможным. Мозг жирафа расположен на 3 м выше сердца.

Ответ: Р > 30 кПа.

3. Нормальное систолическое артериальное давление равно 120 мм рт. ст. Перевести это значение в единицы: а) атм; б) Па.

Ответ: Р = 0,16 атм.

4. Определить минимальное значение направленного вверх ускорения, которое вызывает у человека, с нормальной АД, нарушение кровоснабжение мозга.

Ответ: а=10 м/ .

5. Средняя скорость крови в аорте радиусом 1 см равна 30 см/с.

Выяснить, является ли данное течение ламинарным?

Ответ: число Рейнольдса меньше критического значения, поэтому течение будет ламинарным.

6. Определить максимальную массу крови, которая может пройти за 1 с через аорту при сохранении ламинарного характера течения. Диаметр аорты D = 2 см, а вязкость η = 4 .

Ответ: m=0,18 кг.

Физические основы гемодинамики. Основные понятия и формулы.

1. Условие неразрывности струи:

2. При ламинарном течении жидкости произведение площади S сечения участка, через который она протекает, на ее скорость ʋ является постоянной величиной для данной трубки тока.

3. Уравнение Бернулли:

где ρ — плотность идеальной жидкости; ʋ — скорость ее течения; Р- статическое давление; h — высота расположения центра выделенного сечения потока жидкости.

4. Формула Ньютона, определяющая силу внутреннего трения в движущейся жидкости:

где η — вязкость жидкости; S — площадь соприкосновения слоев движущейся жидкости; — градиент скорости (скорость сдвига).

5. Ньютоновская жидкость — жидкость, вязкость которой не зависит от градиента скорости. Неньютоновская жидкость — жидкость, вязкость которой зависит от градиента скорости и давления.

6. Формула Пуазейля:

где V — объем вязкой жидкости, ламинарно протекающей по участку гладкой трубы длиной L и радиусом r за время t; — давление соответственно в начале и конце выделенного участка.

7. Формула Гагена — Пуазейля:

где Q — объемная скорость жидкости; Х — гидравлическое сопротивление,

8. Число Рейнольдса:

где d — диаметр трубы, по которой со скоростью ʋ течет жидкость плотностью и вязкостью η.

9. Формула Моенса — Кортевега:

где ʋ — скорость распространения пульсовой волны; Е — модуль упругости стенок сосуда; h — толщина стенок сосуда; ρ — плотность жидкости в сосуде; d — диаметр сосуда.

Задачи.

1. При быстром подъеме в самолете человек ощущает щелчки в ушах. Это происходит в тот момент, когда давление за барабанной перепонкой уравнивается с наружным давлением. Если бы этого не происходило, то какая сила действовала бы на барабанную перепонку площадью 0,5 при подъеме на 1000 м?

Решение

В первом приближении давление воздуха при подъеме убывает по закону

Р= ,

ρ=1,29 кг/ — плотность воздуха у поверхности Земли.

Па — давление атмосферы.

|

/ ) Па,

F= =12 500 = 0,63 Н.

Ответ: F= 0,63 Н.

2. Нормальное систолическое артериальное давление равно 120 мм рт. ст. Перевести это значение в единицы: а) атм; б) Па.

Решение

1 мм рт. ст. = ρgh = 132,6

1 атм = 760 мм рт. ст. = 101 кПа;

120 мм рт. ст. = 120 133=16 000 Па = 0,16 атм.

Ответ: Р = 16 000 Па = 0,16 атм.

3. Какова должна быть высота столба жидкости в капельнице, чтобы лекарство поступало в вену под избыточным давлением 60 мм рт. ст.? Давление в вене на 18 мм рт. ст. выше атмосферного. При какой высоте остаточного столба в трубке поступление препарата плотностью ρ=1 г/ прекратится?

Решение

При вливаниях через капельницу лекарство поступает в вену за счет гидростатического давления жидкости.

.

мм рт. ст. = 10 400 Па.

.

Лекарство перестает поступать в вену, когда его давление уравняется с давлением в ней: мм рт. ст. = 2400 Па.

= 0,25 м.

Ответ: а) . б) = 0,25 м.

4. При каждом сокращении сердце прокачивает примерно 70 крови под средним давлением 105 мм рт. ст. Рассчитать мощность сердца при частоте сокращений n=70 ударов в минуту.

Решение

Работа, совершаемая при одном сокращении, находится по формуле:

Р=105 133 = 14 000 Па; = 70 ; Дж.

Работа за 1 мин: А=n Дж.

Это средняя мощность.

Мощность в течение систолы ( ) больше, так как длительность систолы времени сердечного цикла. Вт.

Ответ: N=1,17 Вт; =3,9 Вт.

5. Вода течет по горизонтальной трубе переменного сечения. Скорость течения воды в широкой части, в горизонтально расположенной трубе переменного сечения, переменного разность статических давлений в широкой и узкой части трубы ∆Р = Р₁ – Р₂ =1,82 кПа, Определите скорость течения воды в узкой части трубы.

Решение. Обозначим ρ — плотность воды, запишем уравнение Бернулли для данного случая: /2 + Р₂ = / 2 + Р₁ ,

Выразим из него искомую величину :

Подставив в полученную формулу численные значения входящих в нее величин, получим .

Ответ: .

6. По артерии диаметром d=4 мм течет кровь со скоростью ʋ=0,4 м/с. Определите кинетическую энергию минутного объема крови.

Решение.

Искомая кинетическая энергия (Е) определяется по формул:

где m- масса крови в минутном объеме V, m = ρV = ρQt = ρSʋt, здесь ρ = 1,05 — плотность крови; Q = Sʋ — объемная скорость крови; — площадь сечения сосуда; t = 60 с — время

Таким образом, искомая величина рассчитывается по формуле

Ответ: 0,025 Дж.

7. Скорость пульсовой волны в некоторой артерии ʋ=10 м/с. Чему равен модуль упругости Е этого сосуда, если диаметр d просвета сосуда в 9 раз больше толщины его стенки? Плотность ρ жидкости в сосуде считайте равной плотности воды.

Решение. Из формулы Моенса — Кортевега выразим искомую величину и подставим численные значения:

Ответ: 0.81 МПа.

8. На участке артерии длиной L=1 см и диаметром d=4 мм гидравлическое сопротивление кровотоку Х = 8 Па (с/ ). Каково значение вязкости крови η на этом участке сосуда?

Решение. Преобразование формулы для гидравлического сопротивления позволяет сразу получить необходимое выражение для расчета вязкости крови:

Ответ: 5 мПа с.

Самоконтроль по ситуационным задачам:

1. Ламинарным или турбулентным будет движение крови в аорте, если скорость движения крови 0,5 м/с, диаметр сосуда 8 мм (ρ= 1050 кг\м³, ŋ= 5000мкПа, Rе= 1160)?

Ответ: 840 1160- ламинарное.

2. Определить максимальное количество крови, которое может пройти через аорту за единицу времени, чтобы течение сохранилось ламинарным. Диаметр аорты 0,2 см, вязкость крови 5 мПа∙С, число Рейнольдса 1000.

Ответ: 2,3 мл.

3. Сравнить гидравлическое сопротивление аорты (d= 8 мм), артерии (d= 1,5мм), артериолы (d= 0,04мм) и капилляра(d= 0,008мм) на участке сосуда длиной 50см, если вязкость крови равна 0,004 Па∙с.

Ответ: в порядке убывания: капилляр, артериола, артерия, аорта.

4. Широкий сосуд разветвляется на два параллельных мелких, имеющих гидравлическое сопротивление Х₁= 5 и Х₂= 10. Найти гидравлическое сопротивление системы.

Ответ: 3,33.

Тема №10.Определение коэффициента поверхностного натяжения методом отрыва кольца.

Формы работы:

Вопросы для самоподготовки:

1. Какая жидкость называется смачивающей жидкостью? Приведите пример.

2. Какая жидкость называется несмачивающей жидкостью? Приведите пример.

3. В чем заключается явление поверхностного натяжения?

4. Что такое сила поверхностного натяжения и как она направлена?

5. Что такое газовая эмболия? Нарисуйте и объясните данное явление.

6. Что такое Лапласово давление?

7. Как ведет себя смачивающая и несмачивающая жидкости в капилляре? Изобразите на рисунке.

Перечень практических умений по изучаемой теме:

• иметь представление о различных методах определения коэффициента поверхностного натяжения;

• иметь практические навыки работы с торсионными весами;

• уметь решать практические задачи по определению коэффициента поверхностного натяжения.

Подготовка материалов по темам УИРС:

1. Использование поверхностно-активных веществ в фармации.

2. Использование явления флотации в химической промышленности и медицине.

Самоконтроль по тестовым заданиям данной темы

Выберите правильный ответ

1. Смачивающие жидкости имеют мениск

1) выпуклый

2) вогнутый

2. Дополнительное давление под сферической поверхностью жидкости определяется формулой

1)

2)

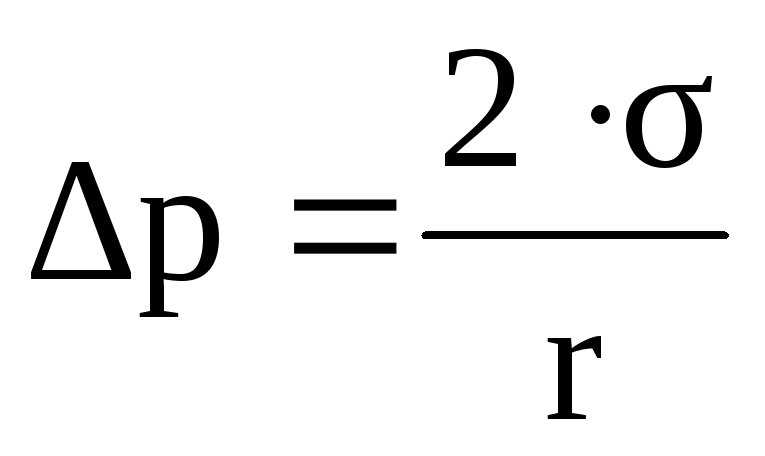
3)

4) P=ρAv

3. Если увеличить длину контура, ограничивающего жидкость, то коэффициент поверхностного натяжения

1) увеличится

2) уменьшится

3) не изменится

4. При выпуклом мениске выполняется соотношение:

1) Рм=Р+∆Рм

2) Рм=Р-∆Рм

3) Рм= ∆Рм

4) Рм=Р

5. При увеличении площади поверхности жидкости коэффициент поверхностного натяжения

1) увеличивается

2) уменьшается

3) не изменяется

6. Жидкость, имеющая постоянный объем, при отсутствии внешних сил стремится занять площадь поверхности

1) минимальную

2) максимальную

7. При увеличении температуры поверхностное натяжение:

1) увеличивается

2) уменьшается

3) не изменяется

8. Равнодействующая сила, действующая на молекулу в поверхностном слое, направлена

1. по касательной к границе раздела жидкости и пара

2. внутрь жидкости

3. внутрь пара

4. под углом 45º к границе раздела

8. Молекулярным называется давление, оказываемое поверхностным слоем на

1) пар

2) жидкость

3) одновременно пар и жидкость

8. Молекулярное давление по величине

1) велико

2) мало

3) равно 0

8. Поверхностная энергия обусловлена работой по перемещению молекулы из

   1. поверхностного слоя в глубину жидкости

   2. глубины жидкости в поверхностный слой

   3. поверхностного слоя в пар

   4. пара в поверхностный слой жидкости

9. Порядок величины молекулярного давления составляет

1)10²

2) 10⁴

3) 10⁶

4) 10⁸

8. При уменьшении радиуса кривизны мениска добавочное давление

1) увеличивается

2) уменьшается

3) не изменяется

Fizika_2_semestr — Стр 2

З А Д А Н И Е № 9

Распространение потенциала действия по безмякотному волокну осуществляется:

A. За счет локальных токов, возникающих между соседними участками, и с затуханием.

B. Сальтоторно, от одного перехвата Ранвье к другому.

C. Без затухания и с ростом величины потенциала действия.

D. Сальтоторно и с ростом величины потенциала действия.

E. С ростом величины потенциала действия.

З А Д А Н И Е № 10

Как соотносятся проницаемости для ионов K⁺, Na⁺, Cl^— при возбуждении мембраны биологической клетки?

A. P(K⁺):P(Na⁺):P(Cl^—)=1 : 0,04 : 0,45

B. P(K⁺):P(Na⁺):P(Cl^—)=1 : 20 : 0,45

C. P(K⁺):P(Na⁺):P(Cl^—)=1 : 0,45 : 20

D. P(K⁺):P(Na⁺):P(Cl^—)=20 : 0,45 : 0,4

E. P(K⁺):P(Na⁺):P(Cl^—)=0.45 : 0,4 : 20

З А Д А Н И Е № 11

Во сколько раз изменится потенциал покоя, если при прочих равных условиях температура окружающей среды увеличится от 36 градусов по Цельсию до 42 ?

A. Не изменится.

B. Уменьшится в 1.17 раза.

C. Увеличится в 1.02 раза.

D. Увеличится в 1.17 раза.

E. Уменьшится в 1.5 раза.

З А Д А Н И Е № 12

Во сколько раз изменится значение потенциала покоя, рассчитываемого по формуле Нернста, если при прочих равных условиях ионы калия заменить на ионы кальция?

A. Не изменится

B. Увеличится в 1.7 раза.

C. Уменьшится в 1.7 раза.

D. Увеличится в 2 раза.

E. Уменьшится в 2 раза.

З А Д А Н И Е № 13

Какие процессы, из перечисленных, можно отнести к активному транспорту ?

A. Переход ионов натрия из клетки в межклеточную среду, ионов калия — внутрь клетки.

B. Переход ионов калия в межклеточную среду.

C. Переход ионов калия и натрия из межклеточной среды внутрь клетки.

D. Переход ионов натрия из межклеточной среды внутрь клетки.

E. Переход ионов натрия и калия из межклеточной среды внутрь клетки.

З А Д А Н И Е № 14

Какие процессы, из перечисленных, можно отнести к пассивному транспорту?

A. Переход ионов натрия из клетки в межклеточную среду.

B. Переход ионов калия из клетки в межклеточную среду, ионов натрия — внутрь клетки.

C. Переход ионов калия и натрия из межклеточной среды внутрь клетки.

D. Переход ионов калия из межклеточной среды внутрь клетки.

E. Переход ионов натрия из клетки в межклеточную среду, ионов калия — внутрь клетки.

З А Д А Н И Е № 15

В состоянии физиологического покоя проницаемость биологической мембраны для различных ионов неодинакова. Как соотносятся проницаемости для ионов К⁺, Nа⁺, Сl^—?

A. P(K⁺):P(Na⁺):P(Cl^—)=1 : 20 : 0,45.

B. P(K⁺):P(Na⁺):P(Cl^—)=0,4 : 1 : 0,45.

C. P(K⁺):P(Na⁺):P(Cl^—)=1 : 0,04 : 0,45.

D. P(K⁺):P(Na⁺):P(Cl^—)=20 : 0,04 : 0,45.

E. P(K⁺):P(Na⁺):P(Cl^—)=0,4 : 20 : 0,45.

ТЕМА: Генез электрограмм (теория)

З А Д А Н И Е № 1

Метод электрокардиографии позволяет определить:

A. Наличие электрического поля сердца.

B. Численные значения разности потенциалов в любой момент времени.

C. Электрический потенциал сердца.

D. Возникновение импульса в синусовом узле.

E. Потенциал действия сердца.

З А Д А Н И Е № 2

Электрический дипольный момент — это векторная величина, определяемая соотношением:

A.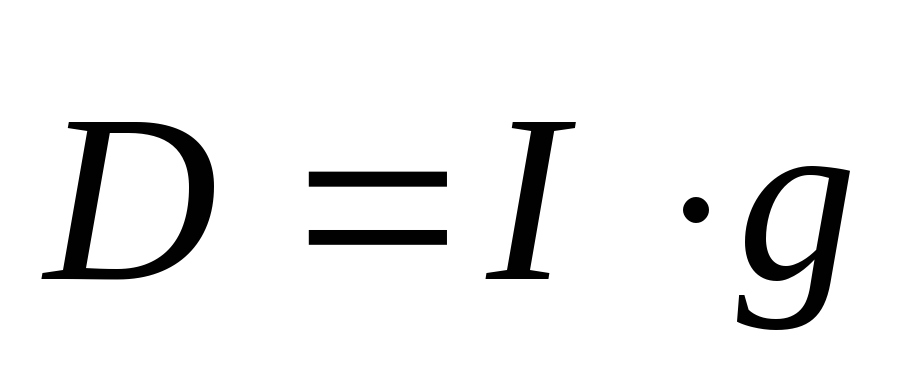

B.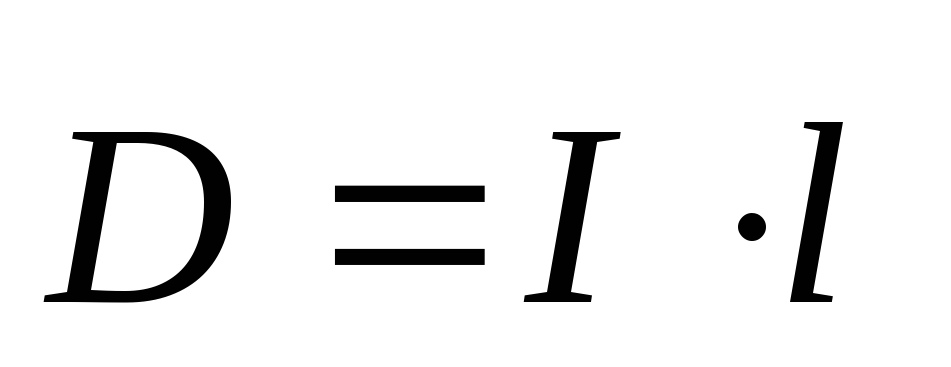

C.

D.

E.

З А Д А Н И Е № 3

Треугольник Эйнтховена образуется соединением точек, расположенных на поверхности:

A. Правой и левой ног и левой руки.

B. Правой и левой ног и правой рук.

C. Правой и левой рук и правой ноги.

D. Правой и левой рук и левой ноги.

З А Д А Н И Е № 4

В первом стандартном отведении регистрируется разность потенциалов между точками, расположенными на:

A. правой и левой руках.

B. правой руке и левой ноге.

C. левой руке и правой ноге.

D. левой руке и левой ноге.

З А Д А Н И Е № 5

Во втором стандартном отведении регистрируется разность потенциалов между точками, расположенными на:

A. правой и левой руках.

B. правой руке и левой ноге.

C. левой руке и правой ноге.

D. левой руке и левой ноге.

З А Д А Н И Е № 6

В третьем стандартном отведении регистрируется разность потенциалов между точками, расположенными на:

A. правой и левой руках.

B. правой руке и левой ноге.

C. левой руке и правой ноге.

D. левой руке и левой ноге.

З А Д А Н И Е № 7

Что является водителем ритма первого порядка?

A. Синусовый узел.

B. Атриовентрикулярный узел(предсердно-желудочковый).

C. Ножки пучка Гиса и их разветвления, включая волокна Пуркинье.

D. Проводящая система предсердий.

E. Проводящая система желудочков.

З А Д А Н И Е № 8

Что является водителем ритма второго порядка?

A. Синусовый узел.

B. Атриовентрикулярный узел(предсердно-желудочковый).

C. Ножки пучка Гиса и их разветвления, включая волокна Пуркинье.

D. Проводящая система предсердий.

E. Проводящая система желудочков.

З А Д А Н И Е № 9

Что является водителем ритма третьего порядка ?

A. Синусовый узел.

B. Атриовентрикулярный узел(предсердно-желудочковый).

C. Ножки пучка Гиса и их разветвления, включая волокна Пуркинье.

D. Проводящая система предсердий.

E. Проводящая система желудочков.

З А Д А Н И Е № 10

Водитель ритма 1-го порядка в норме генерирует импульсы с частотой:

A. 60-80 импульсов в мин.

B. 15-40 импульсов в мин.

C. 40-60 импульсов в мин.

D. 15-80 импульсов в мин.

E. Не генерирует импульсы, а только проводит возбуждение.

З А Д А Н И Е № 11

Водитель ритма 2-го порядка в норме генерирует импульсы с частотой:

A. 60-80 импульсов в мин.

B. 15-40 импульсов в мин.

C. 40-60 импульсов в мин.

D. 15-80 импульсов в мин.

E. Не генерирует импульсы, а только проводит возбуждение.

З А Д А Н И Е № 12

Водитель ритма 3-го порядка в норме генерирует импульсы с частотой:

A. 60-80 импульсов в мин.

B. 15-40 импульсов в мин.

C. 40-60 импульсов в мин.

D. 15-80 импульсов в мин.

E. Не генерирует импульсы, а только проводит возбуждение.

З А Д А Н И Е № 13

Зубец Р электрокардиограммы соответствует:

A. Возбуждению предсердий.

B. Возбуждению желудочков.

C. Реполяризации предсердий.

D. Реполяризации желудочков.

E. Возбуждению предсердий и желудочков.

З А Д А Н И Е № 14

Комплекс QRS электрокардиограммы соответствует:

A. Возбуждению предсердий.

B. Возбуждению желудочков.

C. Реполяризации предсердий.

D. Реполяризации желудочков.

E. Реполярицации предсердий и желудочков.

З А Д А Н И Е № 15

Зубец Т электрокардиограммы соответствует:

A. Возбуждению предсердий.

B. Возбуждению желудочков.

C. Реполяризации предсердий.

D. Процессам реполяризации в сердце.

З А Д А Н И Е № 16

Как ведет себя интегральный электрический вектор сердца на протяжении кардиоцикла?

A. Изменяется по величине и направлению.

B. Не изменяется по величине и направлению.

C. Не изменяется по величине, но изменяется по направлению.

D. Вначале изменяется по величине и, достигнув максимума изменяет направление.

З А Д А Н И Е № 17

Векторэлектрокардиограмма — это:

A. Траектория перемещения конца электрического вектора сердца в трехмерном п ространстве в течении кардиоцикла.

B. Кривая изменения суммарного электрического вектора сердца с течением времени.

C. Кривая, отображающая зависимость от времени разности потенциалов, генерируемых сердцем.

D. Кривая, отображающая зависимость от времени суммарного потенциала, генерируемого сердцем.

З А Д А Н И Е № 18

Каково соотношение между внутренним сопротивлением дипольного эквивалентного электрического генератора и сопротивлением внешней среды?

A. Внутреннее сопротивление источника много больше сопротивления внешней среды.

B. Сопротивление внешней среды много больше сопротивления источника.

C. Сопротивления равны между собой.

D. Внутреннее сопротивление источника в два раза больше сопротивления внешней среды.

З А Д А Н И Е № 19

На электрокардиограмме расстояние между соседними зубцами R составляет 22 мм. Скорость подачи ленты при записи составляла 25 мм/с. Определите длительность кардиоцикла.

A. 0,9 с.

B. 0,3 с.

C. 1,1 с.

D. 4,7 с.

E. 5,5 с.

З А Д А Н И Е № 20

На электрокардиограмме расстояние между соседними зубцами R составляет 30 мм. Скорость подачи ленты при записи составляла 25 мм/с. Определите частоту сердечных сокращений в одну минуту при правильном сердечном ритме.

A. 50 уд./мин.

B. 54 уд./мин.

C. 72 уд./мин.

D. 78 уд./мин.

E. 60 уд./мин.

ТЕМА :Биореология и гемодинамика (теория)

З А Д А Н И Е № 1

Выберите параметры, которые входят формулу Ньютона для силы внутреннего трения.

A. Градиент скорости, площадь взаимодействующих слоев, коэффициент вязкости.

B. Радиус сосуда, разность давлений, коэффициент вязкости, гидравлическое сопротивление.

C. Площадь взаимодействующих слоев, разность давлений, толщина сосуда, скорость.

D. Гидравлическое сопротивление, коэффициент вязкости, скорость.

E. Разность давлений, радиус сосуда, скорость.

З А Д А Н И Е № 2

Выберите параметры, которые входят формулу Пуазейля.

A. Градиент скорости, длина сосуда, коэффициент вязкости.

B. Радиус сосуда, длина сосуда, разность давлений, коэффициент вязкости.

C. Радиус сосуда, длина сосуда, площадь взаимодействующих слоев, коэффициент вязкости.

D. Длина сосуда, площадь взаимодействующих слоев, коэффициент вязкости.

E. Разность давлений, плотность крови, длина сосуда, коэффициент вязкости.

З А Д А Н И Е № 3

Выберите параметры, которые входят формулу для расчета числа Рейнольдса.

A. Площадь взаимодействующих слоев, скорость течения жидкости, плотность жидкости, коэффициент вязкости.

B. Скорость течения жидкости, плотность жидкости, диаметр сосуда, коэффициент вязкости.

C. Градиент скорости, плотность жидкости, коэффициент вязкости.

D. Скорость течения жидкости, разность давлений, диаметр сосуда, длина сосуда.

E. Градиент скорости, плотность жидкости, коэффициент вязкости, диаметр сосуда.

З А Д А Н И Е № 4

Что называют пульсовой волной?

A. Волну, распространяющуюся по кровеносным сосудам (артериям, венам и т.д.) при работе сердца.

B. Распространяющуюся по венам волну повышенного давления.

C. Распространяющуюся по аорте и артериям волну повышенного давления, вызванную выбросом крови из левого желудочка в период систолы.

D. Распространяющуюся по аорте и артериям волну, вызванную скоростью течения крови.

З А Д А Н И Е № 5

От каких параметров зависит скорость пульсовой волны?

A. Модуль упругости, плотность крови, толщина стенки сосуда, радиус сосуда.

B. Коэффициент вязкости, плотность крови, толщина стенки сосуда, радиус сосуда.

C. Градиент скорости, плотность крови, толщина стенки сосуда.

D. Модуль упругости, плотность крови, число Рейнольдса, радиус сосуда.

E. Коэффициент вязкости, площадь взаимодействующих слоев, толщина стенки сосуда, радиус сосуда.

З А Д А Н И Е № 6

Что называют кинематической вязкостью?

A. Отношение вязкости крови к вязкости воды при градиенте давления, равном единице.

B. Отношение динамической вязкости жидкости к плотности жидкости.

C. Отношение динамической вязкости жидкости к вязкости воды при одинаковой температуре.

D. Произведение числа Рейнольдса на скорость течения жидкости.

З А Д А Н И Е № 7

Выберите параметры, от которых зависит характер течения жидкости по сосудам.

A. Плотность жидкости, динамическая вязкость, скорость течения жидкости, радиус сосуда.

B. Плотность жидкости, длина сосуда, скорость течения жидкости, радиус сосуда.

C. Градиент давления, длина сосуда, скорость течения жидкости, радиус сосуда.

D. Гидравлическое сопротивление, длина сосуда, скорость течения жидкости, радиус сосуда.

E. Плотность жидкости, длина сосуда, разность давлений, радиус сосуда.

З А Д А Н И Е № 8

Какие значения скорости соответствуют скорости пульсовой волны в организме человека?

A. 50 см/с

B. 6 м/с , 9 м/с.

C. 30 см/с , 20 м/с, 7 м/с.

D. 20 м/с

E. 5 м/с, 18 м/с.

З А Д А Н И Е № 9

Как изменится гидравлическое сопротивление при увеличении площади сечения трубы в 3 раза?

A. Увеличится в 1.72 раза.

B. Уменьшится в 3 раза.

C. Уменьшится в 4 раза.

D. Уменьшится в 9 раз.

E. Гидравлическое сопротивление не изменится.

З А Д А Н И Е № 10

Коэффициент вязкости для ньютоновских жидкостей зависит от :

A. Температуры, природы жидкости.

B. Скорости ее течения, температуры, природы жидкости.

C. Природы жидкости, скорости течения жидкости.

D. Площади взаимодействующих слоев, природы жидкости.

E. Площади взаимодействующих слоев, градиента скорости.

З А Д А Н И Е № 11

Сила внутреннего трения между двумя слоями жидкости, которые движутся с различными скоростями, зависит от природы жидкости, а также от:

A. Скорости течения жидкости и температуры.

B. Градиента скорости и площади соприкасающихся слоев.

C. Скорости течения жидкости и толщины слоя.

D. Скорости течения жидкости и площади соприкасающихся слоев.

З А Д А Н И Е № 12

Жидкость является неньютоновской, если:

A. Ее вязкость много больше вязкости воды.

B. Ее вязкость много меньше вязкости воды.

C. Ее вязкость зависит от градиента скорости.

D. Ее вязкость не зависит от характера течения жидкости.

З А Д А Н И Е № 13

Как изменяется скорость движения и расход несжимаемой жидкости при движении ее по трубе переменного сечения?

A. С уменьшением сечения трубы скорость движения жидкости увеличивается, а ее расход уменьшается;

B. С уменьшением сечения трубы скорость движения жидкости увеличивается, а ее расход остается неизменным;

C. С уменьшением сечения трубы скорость движения и расход жидкости уменьшаются;

D. С уменьшением сечения трубы скорость движения и расход жидкости увеличиваются;

З А Д А Н И Е № 14

Какой физический смысл коэффициента вязкости?

A. При течении вязкой жидкости, состоящей из крупных молекул, возникают силы, которые и называются коэффициентом вязкости жидкости.

B. Коэффициент вязкости численно равен силе трения, возникающей между слоями единичной площади и градиенте скорости равном единице.

C. Коэффициент вязкости — это отношение вязкости жидкости к вязкости дистиллированной воды при той же температуре.

D. Вязкостью жидкости называют силу, с которой жидкость воздействует на стенки трубы при ее течении.

З А Д А Н И Е № 15

От чего зависит гидравлическое сопротивление вязкой жидкости?

A. От радиуса сосуда, вязкости жидкости, длины сосуда.

B. От скорости течения, вязкости жидкости, длины сосуда.

C. От разности давлений, плотности жидкости, длины сосуда.

D. От разности давлений, плотности жидкости.

E. От скорости течения, вязкости жидкости, числа Рейнольдса.

З А Д А Н И Е № 16

Каким методом определяется вязкость крови?

A. Капиллярным и ротационным.

B. Методом Стокса.

C. Ротационным и методом Стокса.

D. Капиллярным и методом Стокса.

З А Д А Н И Е № 17

Как изменяется градиент давления при движении жидкости по трубе переменного сечения ?

A. Одинаковый по всей длине трубы.

B. Уменьшается по направлению течения жидкости.

C. Больше в трубах большего радиуса.

D. Больше в трубах меньшего радиуса.

З А Д А Н И Е № 18

Какую в среднем работу выполняет сердце за одну систолу?

A. 3.3 Дж

B. 1 Дж

C. 0.68 Дж

D. 5 Дж

E. 33 Дж

З А Д А Н И Е № 19

Какую мощность в среднем развивает сердце?

A. 3.3 Вт

B. 1 Вт

C. 10 Вт

D. 33 Вт

E. 0.55 Вт.

З А Д А Н И Е № 20

Гемодинамика- это:

A. Раздел биомеханики, в котором исследуется движение крови по сосудистой системе.

B. Раздел механики, в котором изучается движение вязкой жидкости.

C. Раздел физики, в котором изучаются основы работы технических устройств, используемых при рассмотрении проблем кровообращения.

D. Раздел медицины, изучающий модели кровообращения.

З А Д А Н И Е № 21

В каких единицах измеряется динамическая вязкость жидкости в системе СИ?

A. м/с

B. Стокс

C. Пуаз

D. Па·с

E. Н/м

З А Д А Н И Е № 22

Что определяется числом Рейнольдса при движении вязкой жидкости по трубе?

A. Скорость течения жидкости.

B. Характер течения жидкости.

C. Величина отношения кинематической вязкости к динамической.

D. Гидравлическое сопротивление трубы.

E. Объем протекающей жидкости.

З А Д А Н И Е № 23

Почему кровь является неньютоновской жидкостью?

A. Это обусловлено наличием в ней форменных элементов.

B. Это обусловлено тем, что для крови число Рейнольдса принимает критическое значение.

C. Это обусловлено большим коэффициентом вязкости крови.

D. Это обусловлено маленьким коэффициентом вязкости крови.

З А Д А Н И Е № 24

Что является причиной движения крови по сосудистому руслу?

A. Работа сердца.

B. Всасывающее действие струи.

C. Разность давлений внутри и вне сосуда.

D. Разность давлений в начале и в конце сосудистого русла.

E. Всасывающее действие струи и работа сердца.

З А Д А Н И Е № 25

Почему скорость течения крови в капиллярах меньше в сравнении со скоростью ее движения в венах, артериях и артериолах?

A. Это связано с тем, что общее сечение (просвет) капилляров максимально.

B. Это связано с тем, что капилляры имеют наименьший просвет.

C. Это связано с тем, что капилляры находятся очень далеко от места выброса крови (левого желудочка).

D. Это связано с тем, что капилляры имеют очень большое гидравлическое сопротивление.

З А Д А Н И Е № 26

При измерении давления по методу Короткова прослушиваются характерные тоны и шумы. Почему они пропадают при снижении давления в манжете ниже диастолического?

A. Это связано с тем, что в этом случае не образуется стоячая волна.

B. Это связано с уменьшением колебаний давления в пульсовой волне.

C. Это связано с резким уменьшением работы, выполняемой сердцем.

D. Это связано с тем, что течение крови через сдавленную артерию переходит от турбулентного к ламинарному.

З А Д А Н И Е № 27

На что затрачивается работа, совершаемая сердцем?

A. Только на преодоление сил давления.

B. На преодоление сил давления и сообщение крови кинетической энергии.

C. На поддержание давления в кровеносной системе.

D. Только на сообщение крови кинетической энергии.

З А Д А Н И Е № 28

На чем основан ультразвуковой метод измерения скорости кровотока?

A. Метод основан на измерении изменения частоты ультразвуковой волны при отражении ее от пульсовой волны.

B. Метод основан на измерении затухания ультразвука при прохождении его через кровеносный сосуд.

C. Метод основан на измерении изменения частоты ультразвуковой волны при отражении ее от движущихся эритроцитов.

D. Метод основан на измерении частоты стоячей ультразвуковой волны при движущихся эритроцитах.

З А Д А Н И Е № 29

Что называют расходом жидкости?

A. Это скорость жидкости, с которой она протекает через сечение трубы.

B. Это масса жидкости, протекающая через сечение трубы.

C. Это объем жидкости, протекающий по системе труб (сосудов).

D. Это объем жидкости, протекающий через сечение трубы в единицу времени;

ЗАДАЧИ

З А Д А Н И Е № 1

Вычислите силу трения, действующую на S=4 кв.м. дна русла, если по нему перемещается поток воды высотой h=2м, скорость верхнего слоя воды равна 0 у дна, вязкость жидкости n=10(Па · с).

A. 0.6 мН

B. 6.72 Н

C. 0.3 мкН

D. 320 кН

E. 4.7 Н

З А Д А Н И Е № 2

На каждый квадратный метр площади дна канала, по которому протекает вода действует сила 0.63 мН. Определить высоту движущегося потока воды, если скорость верхних слоев воды 0.5 м/с, а затем постепенно убывает и у дна становится равной 0. Вязкость воды 1.787·10 Па·с.

A. 8.5 м

B. 1.42 м

C. 0.79 м

D. 1 м

E. 0.52 м

З А Д А Н И Е № 3

Скорость течения воды в широкой части горизонтальной водопроводной трубы равна 50 см/с. Какова скорость течения воды в узкой части той же трубы, диаметр которой в четыре раза меньше?

A. 12.5 м/с

B. 25 см/с

C. 4.0 м/с

D. 8.0 м/с

E. 12.5 см/с

З А Д А Н И Е № 4

Определить объемную скорость течения воды в трубе, если диаметр трубы 4 см, а скорость течения воды 15см/с.

A. 188.4 см/с

B. 67 см/с

C. Для решения задачи не хватает данных

D. 1008 см/с

E. 214 см/с

З А Д А Н И Е № 5

При стационарном потоке крови в сосуде с переменным сечением в сечении 2 квадратных сантиметра скорость потока равна 35 см/с. Какова скорость кровотока в сечении площадью 2.5 см.

A. 75 см/с.

B. 18.75 м/с.

C. 43.75 см/с.

D. 28 см/с.

E. 14 см/с.

З А Д А Н И Е № 6

Как изменится гидравлическое сопротивление при увеличении площади сечения трубы в 3 раза?

A. Увеличится в 1.73 раза.

B. Уменьшится в 3 раза.

C. Уменьшится в 1.73 раза.

D. Нет, не изменится, т.к. гидравлическое сопротивление не связано с площадью сечения трубы.

E. Уменьшится в 9 раз.

З А Д А Н И Е № 7

Каково гидравлическое сопротивление кровеносного сосуда длиной 12 см и радиусом 0,1 мм. (Вязкость крови 5 мПа·с).

A. 1,53·10 Па·с/м.

B. 2,45·10 Па·с/м.

C. 1,89·10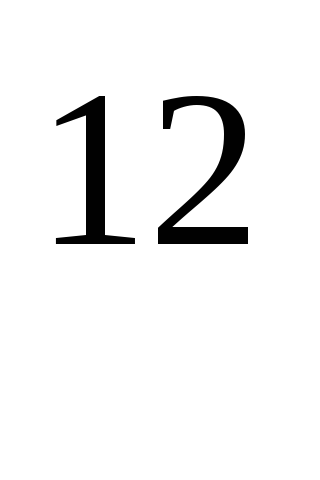 Па·с/м.

D. 3,06·10 Па·с/м.

E. 4,89·10 Па·с/м.

З А Д А Н И Е № 8

Как изменится гидравлическое сопротивление сосуда, если вязкость крови уменьшится в 1.5 раза?

A. Уменьшится в 1.5 раза.

B. Увеличится в 1.5 раза.

C. Увеличится в 3 раза.

D. Не изменится.

E. Уменьшится в 2.25 раза.

З А Д А Н И Е № 9

Какова длина кровеносного сосуда, если его гидравлическое сопротивление 1,53·10 Па·с/м и радиусом 0,1 мм.(Вязкость крови 4 мПа·с).

A. 15 см.

B. 1,5 м.

C. 3,5 см.

D. 6,5 м.

E. 5 см.

З А Д А Н И Е № 10

Скорость пульсовой волны в артериях составляет 10 м/с. Чему равен модуль упругости этих сосудов, если известно, что отношение радиуса просвета к толщине стенки сосуда равна 8, а плотность крови равна 1.05·10 кг/м.

A. 8·10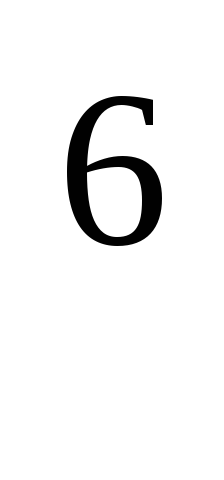 Па

B. 1.67·10 Па

C. 2.3·10 Па

D. 1.07·10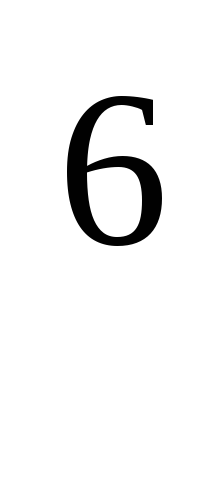 Па

E. 2.8.06·10 Па

З А Д А Н И Е № 11

Как изменится скорость пульсовой волны, если толщина стенки сосуда станет в 2 раза больше?

A. Увеличится в 2 раза.

B. Уменьшится в 1.4 раза.

C. Не изменится.

D. Увеличится в 1.41 раза.

E. Уменьшится в 4 раза.

З А Д А Н И Е № 12

Определить отношение радиуса просвета к толщине стенки сосуда, если известно, что скорость пульсовой волны в артериях составляет 8 м/с, модуль упругости этих сосудов 0,8·10 Па, а плотность крови 1050 кг/м.

A. 3.6

B. 5.95

C. 0.54

D. 8.6

E. 2.54

З А Д А Н И Е № 13

Как изменится скорость распространения пульсовой волны в сосуде при изменении плотности крови от 1.1 г/см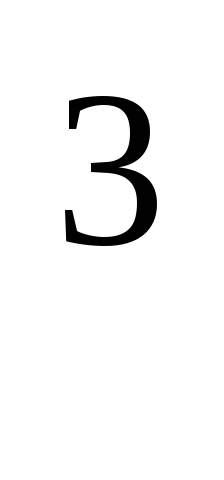 до 1 г/см.

A. Не изменится.

B. Увеличится в 1.05 раза.

C. Уменьшится в 1.25 раза.

D. Уменьшится в 1.05 раза.

E. Увеличится в 1.25 раза.

З А Д А Н И Е № 14

Как изменится скорость распространения пульсовой волны в сосуде при изменении толщины стенки сосуда от 0.4 мм до 0.5 мм.

A. Не изменится

B. Увеличится в 1.25 раза.

C. Уменьшится в 1.1 раза.

D. Увеличится в 1.1 раза.

E. Уменьшится в 1.25 раза.

З А Д А Н И Е № 15

Определить максимальное количество крови, которое может пройти через аорту за две секунды, чтобы течение сохранялось ламинарным. Диаметр аорты D=2 см, вязкость крови равна 5·10^-3 Па·с, число Рейнольдса Re=2300.

A. 0.5 кг

B. 0.45 кг

C. 0.25 кг

D. 0.36 кг

E. 0.18 кг

З А Д А Н И Е № 16

Определите диаметр артерии, если через нее проходит за две секунды кровь массой 20г. Течение крови считать ламинарным. Число Рейнольдса равняется 1000. Вязкость крови принять равной 4х10^-3 Па·с.

A. 1.5 см

B. 3.2 мм

C. 6.1 мм

D. 2.7 см

E. 1.6 мм

З А Д А Н И Е № 17

Определите число Рейнольдса, если через аорту диаметром 3 см за 2 секунды проходит 200 г крови при вязкости крови 5 мПа·с.

Методические указания и контрольные задания для студентов-заочников 2 курса по специальности 040500 «фармация» Волгоград-2002 (стр. 5 из 12)

39. 2 моль кислорода расширяются от начального давления 400 кПа против постоянного внешнего давления 100 кПа. Газ находится при температуре 22⁰С. Найдите конечный объем кислорода.

40. Азот нагревался при постоянном давлении, причем ему было сообщено количество теплоты равное 21 кДж. Определить работу, которую совершил газ, и изменение его внутренней энергии.

41. С какой высоты упала большая капля воды массой 2г, если она разбилась на мелкие капли радиусом 10^-5см?

42. Из капельницы заставили вытекать каплями равные массы воды (сначала холодной при температуре 10°С, затем горячей – при 63°С). Во сколько раз измениться коэффициент поверхностного натяжения воды, если в первом случае было 30 капель, а во втором – 34? Плотность воды считать неизменной, т.е. пренебречь тепловым расширением воды.

44. В двух капиллярных трубках разного диаметра, опущенных в воду, установилась разность уровней 2.6 см. При опускании этих же трубок в спирт разность уровней 2.6 см. При опускании этих же трубок в спирт разность уровней оказалась 1 см. Зная, что для воды s =73 мН/м, найти коэффициент поверхностного натяжения спирта. Плотность воды – 1000 кг/м³, спирта – 790 кг/м³.

45. Найти массу воды, поднявшейся по капиллярной трубке диаметром 0.5 мм. Плотность воды 1000 кг/м³, s =73 мН/м.

46. Для определения коэффициента поверхностного натяжения воды была использована пипетка с диаметром выходного отверстия 2 мм. Масса 40 капель оказалась равной 1.9 г. Найти s.

47. Разность уровней (s =500 мН/м) ртути в сообщающихся стеклянном капилляре и широком сосуде равна 7.4 мм. Определите радиус кривизны мениска ртути.

48. В горизонтально расположенный капилляр набирается 0.25 мл крови так, что образуется столбик длиной 10 см. Вытечет ли кровь из капилляра, если его поставить вертикально?

49. В кровеносном сосуде образовался пузырек воздуха. В результате течения крови пузырек воздуха деформировался, образовав поверхности с радиусами кривизны 0.1 и 0.5 мм. Определить дополнительное давление в сосуде, возникающее в результате деформации пузырька воздуха. Для крови s =58 мН/м, r = 1050 кг/м³.

50. Из трубки диаметром 1.6 мм капает этиловый спирт (s =22.3 мН/м, r = 720 кг/м³). Сколько капель приходится на 1 г спирта? Диаметр шейки капли в момент отрыва считать равным диаметру трубки.

51. Шарик радиусом 3мм движется в вертикальной трубке, заполненной глицерином. Определить силу сопротивления глицерина, если время падения шарика в трубке длиной 80 см равно 10 с. Плотность и вязкость глицерина соответственно равны 1260 кг/м³ и 1.48 Па^.с.

52. Подача воды в теплице производится с помощью горизонтальной трубы длиной 20 м и диаметром 6 см, один конец которой вварен в нижнюю часть боковой поверхности бака радиусом 2м и высотой 5 м. Найти скорость понижения воды для случая его полного заполнения. Плотность и вязкость воды соответственно равны 1000 кг/м³ и 1 мПа^.с.

53. У человека в покое величина кровотока на 100 г мышц руки в среднем 2.5 мл в минуту. Определить количество капилляров в тканях мышц, считая, что длина каждого из них составляет 0.3 мм, а диаметр 10 мкм. Разность давлений на концах капилляров принять равной 33.3^.10² Па.

54. Определить скорость оседания эритроцитов в плазме крови (в мм/ч) исходя из предположения, что они имеют форму шариков диаметром 7 мкм и не склеиваются между собой. Плотность эритроцитов 1090 кг/м³, плотность крови 1050 кг/м³, вязкость крови 5 мПа^.с.

55. Через иглу, надетую на трубку длиной 20 см, выливается кровь из ампулы диаметром 75 мм. Определить, через какое время из ампулы выльется 250 мл крови, если диаметр иглы 1 мм, а длина 4 см. Ампула содержит 500 мл крови. Трубка и ампула расположены вертикально. Плотность крови 1050 кг/м³, вязкость крови 5 мПа^.с.

56. Диаметр поршня шприца 20 мм, площадь отверстия иглы 0.5 мм². Сколько времени будет вытекать из горизонтально расположенного шприца раствор новокаина вязкостью 1.24 мПа^.с, если действовать на поршень силой 4 Н? Ход поршня 4 см, длина иглы 4 см.

57. Определить, сколько процентов от суточного расхода энергии человека (11500 кДж) затрачивается сердцем на перемещение крови при частоте пульса 70 уд/мин, учитывая, что среднее давление в левом желудочке равно 12 кПа, а в правом в шесть раз меньше. Количество крови, выбрасываемое каждым желудочком, считать равным 60 мл, а скорость кровотока в обоих случаях 0.4 м/с.

58. Определите максимальное количество крови, которое может пройти через аорту в 1 с, чтобы течение сохранялось ламинарным. Диаметр аорты 2 см, вязкость крови 5 мПа^.с.

59. Определить работу сердца человека в покое при одном сокращении и его мощность, если среднее давление, при котором кровь выбрасывается в аорту левым желудочком, равно 133.3^.10² Па, ударный объем 60 мл, скорость крови в аорте 0.5 м/с. Работа правого желудочка составляет примерно 0.2 работы левого желудочка, а время их сокращения 0.3 с. Плотность крови 1050 кг/м³, вязкость крови 5 мПа^.с.

60. Определить линейную скорость кровотока в аорте радиусом 1.5 см, если при длительности систолы 0.25 с через аорту протекает 60 мл крови. Во сколько раз эта скорость меньше критической? Плотность крови 1050 кг/м³, вязкость крови 5 мПа^.с.

61. Колебательное движение материальной точки задано уравнением:

.

Найти зависимость кинетической и потенциальной энергии от времени. Определить амплитуду, период, начальную фазу, максимальную скорость и максимальное ускорение материальной точки.

62. Два одинаково направленных колебания заданы уравнениями:

x₁ = 3cos5(t+0.04p) x₂ = 5cos5(t+0.14p)

Запишите уравнение результирующего колебания.

63. Материальная точка массой 5 г колеблется согласно уравнению x=10cos(2t+j₀). Найдите максимальную силу, действующую на точку, и полную энергию.

64. Логарифмический декремент затухания камертона, колеблющегося с частотой 100 Гц, равен 0.002. Через какой промежуток времени амплитуда колебаний камертона уменьшится в 100 раз?

65. Определите частоту собственных колебаний системы, если при уменьшении коэффициента затухания в 2 раза резонансная частота изменяется от 3.88 с^-1 до 3.97 с^-1.

66. Груз массой 2.5 кг, подвешенный к пружине с жесткостью 3.6^.10² Н/м, совершает вынужденные колебания под действием внешней силы F=13.5sin6t. Найти амплитуду вынужденных колебаний груза. Трением пренебречь.

67. Определите резонансную частоту ноги человека при маховых движениях, рассматривая ее как физический маятник с приведенной длиной 38.8 см.

68. Насос для перекачки крови в аппарате «искусственное сердце» имеет диафрагму массой 10 г, совершающую затухающие колебания, описываемые уравнением x =0.4е^—t sin4pt (см). Под действием внешней периодической силы ее колебания стали описываться уравнением x=sin(2pt+j) (см). Записать уравнение внешней периодической силы. Какова разность фаз между действующей силой и смещением?

69. Определить коэффициент затухания колебаний аналитических весов, если известно, что за 5с величина амплитуды уменьшилась в 10 раз.

70. Частота свободных колебаний тела массой 2 г равна 100 Гц. Определить коэффициент затухания, если запас энергии в течение 30с уменьшился на 20%. Чему равен коэффициент сопротивления среды и логарифмический декремент затухания?

71. Плоская звуковая волна распространяется в воде. Записать уравнение волны смещения и давления, если максимальное смещение частиц среды равно 5.10^-4 м и их амплитудное значение скорости 150 м/с при температуре 20⁰ С.

72. Автомобильная сирена издает звук частотой 800 Гц. Какой частоте колебаний будет соответствовать звук сирены для неподвижного наблюдателя при приближающемся и удаляющемся автомобиле, если скорость его 90 км/ч?

73. Определить скорость движения передней стенки желудочка сердца в сторону груди, если при эхолокации ультразвуком частотой 800 кГц отраженный сигнал воспринимался на частоте 800.21кГц. Скорость ультразвука в тканях принять равной 1540 м/с.

74. Определить интенсивность сердечных тонов у входа в воронку стетоскопа диаметром 6 см, если на барабанную перепонку площадью 70 мм² попадает 74% звуковой энергии при интенсивности 10^-15 Вт/см².

75. Определить величину смещения барабанной перепонки уха человека на пороге слышимости для звука частотой 1 кГц, если максимальные скорости смещения перепонки и частиц воздуха одинаковы и равны 5^.10^-6 см/с. Сравнить величину смещения барабанной перепонки с размерами атома.

76. Определить амплитудное значение давления в ткани организма на глубине 2 см при облучении ее интенсивностью 2 Вт/см². Коэффициент поглощения ткани считать равным 0.19 см^-1, а ее плотность 1.06 г/см³.

77. Источник звука совершает колебания по закону x = sin2000pt. Скорость распространения звука 340 м/с. Запишите уравнение колебаний для точки на расстоянии y=102м от источника. Потерями энергии пренебречь, волну считать плоской.

78. Точка, находящаяся на расстоянии y=0.5м от источника колебаний, имеет в момент t=T/3 смещение, равное половине амплитуды. Найдите длину волны, если при t=0 смещение источника равно нулю.

79. Разность хода звуковых волн, приходящими в левое и правое ухо человека, составляет 1 см. Определить сдвиг фаз между обоими звуковыми ощущениями для тона с частотой 1000 Гц. Скорость звука в воздухе 340м/с.

Сайт учителей биологии МБОУ Лицей № 2 города Воронежа

Движение крови по сосудам   Кровяное давление — это давление крови на стенки кровеносных сосудов организма. Это давление создаётся в результате сокращений желудочков сердца и выброса из них крови, а также сопротивления току крови в сосудистом русле. Величина давления в кровеносной системе непостоянна и зависит от фазы сердечного цикла. Максимального уровня артериальное давление достигает во время сокращения (систолы) левого желудочка сердца. При этом из сердца выталкивается 60 — 70 мл крови. Такое количество крови не может пройти сразу через мелкие кровеносные сосуды (особенно капилляры), поэтому эластичная аорта растягивается, а давление в ней повышается (систолическое давление). В норме оно достигает в крупных артериях 100 — 140 мм рт. ст. Во время паузы между сокращениями желудочков сердца стенки кровеносных сосудов (аорты и крупных артерий), будучи растянутыми, начинают сокращаться и проталкивать кровь в капилляры. Давление крови постепенно падает и к концу диастолы достигает минимальной величины (60 — 80 мм рт. ст. в крупных артериях) — диастолическое давление. Разница в величине систолического и диастолического давления называется пульсовым давлением и является важным показателем нормальной работы сердца. Для медицинских целей артериальное давление измеряют в плечевой артерии с помощью специального прибора — тонометра, по методу, предложенному в 1905 году русским хирургом Н. С. Коротковым. Он заключается в следующем: в манжете создаётся давление, при котором ток крови в плечевой артерии полностью прекращается. Затем оно постепенно снижается, и одновременно фонендоскопом в локтевой ямке выслушиваются возникающие звуки. В тот момент, когда давление в манжете становится немного ниже, чем систолическое, появляются короткие ритмические звуки. Они обусловлены прохождением порций крови под манжетой в период систолы. По мере снижения давления в манжете интенсивность тонов уменьшается, и при его определённой величине они исчезают. В этот момент давление в ней примерно соответствует диастолическому. Давление крови в кровеносных сосудах уменьшается по мере удаления от сердца. Наибольшее давление — в аорте, где оно составляет 140/90 мм рт. ст. (первая цифра обозначает систолическое давление, а вторая — диастолическое), в то время как в наиболее крупных венах (верхняя и нижняя полые вены) кровяное давление может быть отрицательным. В норме величина кровяного давления зависит от индивидуальных особенностей, образа жизни, рода занятий. Величина его изменяется с возрастом, возрастает при физической нагрузке, эмоциональном напряжении и т. д. Однако у лиц, систематически занимающихся тяжёлым физическим трудом, а также у спортсменов величина систолического давления может уменьшаться и составлять 100 — 90 мм рт. ст., а диастолического — 60 — 50 мм рт. ст. Давление мало зависит от пола, но зато изменяется с возрастом. Ученые опытным путем установили формулу, по которой каждый человек до 20 лет может рассчитать свое нормальное давление в состоянии покоя. (Людям старше этого возраста приходится применять другую формулу.) АД верхнее = 1,7 x возраст + 83. АД нижнее = 1,6 x возраст + 42. (АД – артериальное давление, возраст берется в целых годах.) Если вам, например, 15 лет, то верхнее давление равно 110, а нижнее 65 мм рт. ст. Обычно артериальное давление изображают в виде дроби, числитель которой указывает верхнее давление, знаменатель нижнее, т. е. в данном случае АД = 110/65. Реальное давление здорового человека не всегда соответствует расчетному. Как и большинство физиологических показателей, оно может колебаться. Особенно подвержено колебаниям верхнее давление, нижнее отличается большей стабильностью. У здоровых людей при нагрузках поднимается верхнее давление, нижнее же меняется незначительно. То же может произойти при волнении, а вот в состоянии глубокого сна давление падает и даже опускается несколько ниже нормы. Измеряют артериальное давление утром, натощак, так как после еды давление поднимается. Повышенное давление ведет к гипертонии, пониженное – к гипотонии. Оба заболевания достаточно опасны и требуют лечения, иногда длительного. В подростковом возрасте давление может быть немного повышенным или пониженным (юношеская гипертония или гипотония). Обычно эти нарушения проходят без лечения, но при слабости, сонливости днем целесообразно показаться врачу. Несмотря на значительные колебания кровяного давления (например, в зависимости от нагрузки, эмоционального состояния и т. д.), в организме существуют сложные механизмы регуляции его уровня, стремящиеся вернуть давление к норме по окончании действия этих факторов. Регуляция кровяного давления Давление крови, как и все процессы в организме, регулируется двояко: нервной системой (нервная регуляция) и гуморально. Нервная регуляция связана с деятельностью сосудодвигательного центра, который состоит из совокупности нейронов, расположенных в спинном, продолговатом мозге, гипоталамусе и коре полушарий большого мозга. Основной сосудодвигательный центр находится в продолговатом мозге и состоит из двух отделов: прессорного и депрессорного. Раздражение первого вызывает сужение артерий и подъём артериального давления, а раздражение второго — расширение артерий и падение давления в них. На тонус сосудистой стенки оказывает влияние вегетативная нервная система. Гуморальная регуляция связана с циркулированием в крови определённых веществ, которые делят на сосудосуживающие и сосудорасширяющие. К первым относят адреналин и норадреналин (гормоны коры надпочечников), вазопрессин (гормон задней доли гипофиза), а также некоторые вещества, образующиеся в слизистой оболочке кишечника, мозге, почках, тромбоцитах и соединительной ткани. К сосудорасширяющим веществам относятся тканевые гормоны (биологически активные вещества, образующиеся в различных тканях организма), молочная кислота, углекислый газ, ионы калия, магния и т. д. Пульс (лат. pulsus — удар, толчок) — периодические, связанные с сокращениями сердца ритмические колебания стенки артериальных сосудов, обусловленные систолическим повышением давления в них. Измерение артериального пульса является одним из важнейших исследований деятельности сердечно-сосудистой системы. Пульс необходимо измерять в состоянии покоя, желательно после сна, до принятия пищи. Основным методом исследования артериального пульса является пальпация — нащупав артерию, её прижимают к подлежащей кости, что позволяет хорошо ощутить артериальный пульс как толчкообразное увеличение объёма артерии. Пульс, как правило, исследуют на лучевой артерии, которая расположена поверхностно и хорошо прощупывается. Для измерения пульса кисть охватывают правой рукой в области лучезапястного сустава так, чтобы большой палец располагался на тыльной стороне предплечья, а остальные пальцы — на передней его поверхности. Нащупав артерию, прижимают её к нижележащим тканям для того, чтобы лучше ощущать пульсовый удар. При пальпаторном исследовании артериального пульса его характеристика основывается на определении частоты пульсовых ударов, а также ритма. Частота пульса — количество пульсовых ударов в единицу времени. Как правило, частоту пульса исследуют в течение 1 минуты. Величина пульса в нормальных условиях соответствует частоте сердечных сокращений и у здоровых людей в норме составляет от 60 до 80 ударов в 1 мин. У лиц, занятых физическим трудом, а также у пожилых людей частота пульса обычно ниже и нередко бывает меньше 60. Пульс учащается после приёма пищи, а также при повышении температуры тела в среднем на 10 ударов на каждый последующий градус. Ритм пульса оценивают по регулярности следующих друг за другом пульсовых волн. У здоровых взрослых людей пульсовые волны, как и сокращения сердца, отмечаются через почти равные промежутки времени, т. е. пульс ритмичен. Если промежутки времени между пульсовыми ударами не равны между собой, это свидетельствует о неритмичном пульсе, что является признаком заболеваний сердца, связанных с нарушением ритма его сокращений. Скорость кровотока В единицу времени к сердцу притекает столько же крови, сколько выходит из его желудочков. Непрерывный поток крови может осуществляться при условии, что одно и то же её количество будет проходить через любой участок поперечного сечения сосудов. Различают линейную и объёмную скорость кровотока. Линейная скорость кровотока — это расстояние, которое проходит частица крови в единицу времени. Скорость крови обратно пропорциональна общей площади поперечного сечения тех сосудов, через которые она проходит в единицу времени. Наибольшая линейная скорость кровотока, составляющая 0,5 — 0,6 м/сек. — в аорте. В артериях она снижается до 0,2 — 0,4 м/сек. Суммарный просвет капиллярного русла в 500 — 600 раз больше, чем аорты, поэтому скорость кровотока в капиллярах уменьшается до 0,5 мм/сек. Замедление тока крови в капиллярах имеет большое физиологическое значение, так как в них происходит обмен веществ между кровью и тканями. Общая площадь поперечного сечения вен будет меньше, чем капилляров, потому что они сливаются, следовательно, в венах кровь будет течь быстрее. В крупных венах линейная скорость кровотока вновь возрастает до 0,1 — 0,2 м/сек. Объёмная скорость кровотока — это количество крови, проходящей через поперечное сечение сосуда за единицу времени. Она зависит от разности давлений в начале и конце сосуда и сопротивления току крови. Полный кругооборот по двум кругам кровообращения кровь совершает за 20-25 с, если человек находится в покое. При физической работе это время еще короче. Перераспределение крови в организме В организме человека постоянно происходит перераспределение крови: к одним органам ее поступает больше, к другим меньше. Если орган работает, то кровь к нему притекает усиленно, принося дополнительный кислород и питательные вещества. В то же время приток крови к неработающим органам уменьшается. Снабжение органов кровью зависит от их деятельности. Французский исследователь Моссо поместил человека на весы так, чтобы одна половина тела уравновешивала другую. После этого испытуемому предложили перемножить несколько двухзначных чисел, испытуемый задумался, и … его голова стала опускаться вниз. Когда задача была решена и весы уравновесились, Моссо предложил лежащему на весах человеку пошевелить пальцами ног. Весы опустились в противоположную сторону, туда, где были ноги. Причина движения крови – разность давлений в начале и конце пути, которое создает сердце. Самое высокое давление в аорте, самое низкое – в полых венах. Давление измеряют в плечевой артерии, утром, натощак. Давление в момент выброса крови в аорту называется верхним (или систолическим), наименьшее давление в момент паузы сердца называют нижним (диастолическим). Заболевание, связанное со стойким понижением давления, называют гипотонией, а со стойким повышением давления – гипертонией. Пульсом называют ритмические колебания стенок артерий. По пульсу можно определить частоту и силу сердечных сокращений. Кровь в организме непрерывно перераспределяется. Наилучшее кровоснабжение получают работающие органы. Скорость крови наибольшая в артериях, наименьшая в капиллярах, в венах снова возрастает. < Предыдущая страница «Регуляция работы сердца»  Следующая страница «Предупреждение заболеваний сердца и сосудов» >

Календарь «  Февраль 2020  » Пн Вт Ср Чт Пт Сб Вс           1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 Статистика Онлайн всего: 8 Гостей: 8 Пользователей: 0