Группа (математика) — Википедия

У этого термина существуют и другие значения, см. Группа.

Гру́ппа в математике — множество, на котором определена ассоциативная бинарная операция, причём для этой операции имеется нейтральный элемент (аналог единицы для умножения), и каждый элемент множества имеет обратный. Ветвь общей алгебры, занимающаяся группами, называется теорией групп^[1].

Один из примеров группы — множество целых чисел, снабжённое операцией сложения: сумма любых двух целых чисел также даёт целое число, роль нейтрального элемента играет ноль, а число с противоположным знаком является обратным элементом. Другие примеры — множество вещественных чисел с операцией сложения, множество вращений плоскости вокруг начала координат. Благодаря абстрактному определению группы через систему аксиом, не привязанной к специфике образующих множеств, в теории групп создан универсальный аппарат для изучения широкого класса математических объектов самого разнообразного происхождения с точки зрения общих свойств их структуры. Вездесущность групп в математике и за её пределами делает их важнейшей конструкцией в современной математике и её приложениях.

Группа фундаментально родственна понятию симметрии и является важным инструментом в изучении всех её проявлений. Например, группа симметрии отражает свойства геометрического объекта: она состоит из множества преобразований, оставляющих объект неизменным, и операции комбинирования двух таких преобразований, следующих друг за другом. Такие группы симметрии, как точечные группы симметрии, помогают понять явление молекулярной симметрии в химии; группа Пуанкаре характеризует симметрию физического пространства-времени, а специальные унитарные группы применяются в стандартной модели физики элементарных частиц^[2].

Понятие группы ввёл Эварист Галуа, изучая многочлены в 1830-е годы^[3].

Современная теория групп является активным разделом математики^[4]. Один из наиболее впечатляющих результатов достигнут в классификации простых конечных групп, которая была завершена в 1981 году: доказательство теоремы составляет десятки тысяч страниц сотен научных статей более ста авторов, опубликованных с 1955 года, но статьи продолжают появляться из-за обнаруживаемых пробелов в доказательстве

[5]. С середины 1980-х годов значительное развитие получила геометрическая теория групп, изучающая конечно-порождённые группы как геометрические объекты.

Непустое множество G с заданной на нём бинарной операцией ∗{\displaystyle {*}}: G×G→G{\displaystyle \mathrm {G} \times \mathrm {G} \rightarrow \mathrm {G} } называется группой (G,∗){\displaystyle (\mathrm {G} ,*)}, если выполнены следующие аксиомы:

1. ассоциативность: ∀(a,b,c∈G):(a∗b)∗c=a∗(b∗c){\displaystyle \forall (a,b,c\in G)\colon (a*b)*c=a*(b*c)};
2. наличие нейтрального элемента: ∃e∈G∀a∈G:(e∗a=a∗e=a){\displaystyle \exists e\in G\quad \forall a\in G\colon (e*a=a*e=a)};
3. наличие обратного элемента : ∀a∈G∃a−1∈G:(a∗a−1=a−1∗a=e){\displaystyle \forall a\in G\quad \exists a^{-1}\in G\colon (a*a^{-1}=a^{-1}*a=e)}.

Последние две аксиомы можно заменить одной аксиомой существования операции обратной ∗{\displaystyle *}:

∀(a,b∈G)∃(x,y∈G):(a∗x=b)∧(y∗a=b){\displaystyle \forall (a,b\in G)\quad \exists (x,y\in G)\colon (a*x=b)\land (y*a=b)}.

При этом вышеприведённые аксиомы не являются строго минимальными. Для существования нейтрального и обратного элементов достаточно наличия левого нейтрального элемента и левого обратного элемента. При этом можно доказать, что они автоматически будут обычным нейтральным и обратным элементами^[6].

Связанные определения[править | править код]

• В общем случае от группы не требуется выполнения свойства коммутативности.
  • Пары элементов a,b{\displaystyle a,\;b}, для которых выполнено равенство a∗b=b∗a{\displaystyle a*b=b*a}, называются перестановочными или коммутирующими.
  • Множество элементов, перестановочных со всеми элементами группы, называется центром группы.
  • Группа, в которой любые два элемента коммутируют, называется коммутативной или абелевой.
• Подгруппа — подмножество H{\displaystyle H} группы G{\displaystyle G}, которое является группой относительно операции, определённой в G{\displaystyle G}.
• Порядок группы (G,∗){\displaystyle (G,*)} — мощность G{\displaystyle G} (то есть число её элементов).
  • Если множество G{\displaystyle G} конечно, то группа называется конечной.
• Гомоморфизмы групп — это отображения групп, которые сохраняют групповую структуру. То есть отображение групп f:(G,∗)→(H,×){\displaystyle f\colon (G,*)\to (H,\times )} называется гомоморфизмом, если удовлетворяет условию f(a∗b)=f(a)×f(b){\displaystyle f(a*b)=f(a)\times f(b)}.
• Две группы называются изоморфными, если существуют гомоморфизм групп f:(G,∗)→(H,×){\displaystyle f\colon (G,*)\to (H,\times )} и гомоморфизм групп g:(H,×)→(G,∗){\displaystyle g\colon (H,\times )\to (G,*)}, такие что f(g(a))=a{\displaystyle f(g(a))=a} и g(f(b))=b{\displaystyle g(f(b))=b}, где b∈G{\displaystyle b\in G} и a∈H{\displaystyle a\in H}. В этом случае эти гомоморфизмы называются изоморфизмами.
• Для элемента g∈G{\displaystyle g\in G} левый смежный класс по подгруппе H{\displaystyle H} — множество gH={gh∣h∈H}{\displaystyle gH=\{gh\mid h\in H\}}, правый смежный класс по подгруппе H{\displaystyle H} — множество Hg={hg∣h∈H}{\displaystyle Hg=\{hg\mid h\in H\}}.
• Нормальная подгруппа — подгруппа особого типа, левый и правый смежные классы по которой совпадают. Для любого g∈G{\displaystyle g\in G}, gH=Hg{\displaystyle gH=Hg}.
• Факторгруппа — множество смежных классов группы по её нормальной подгруппе, само являющееся группой.

Мультипликативная запись[править | править код]

Обычно групповую операцию называют (абстрактным) умножением; тогда применяется мультипликативная запись:

Если групповая операция именуется умножением, то саму такую группу G{\displaystyle \mathrm {G} } при этом называют мультипликативной и при полном способе записи (когда хотят явно указать групповую операцию) обозначают так: (G,⋅){\displaystyle (\mathrm {G} ,\cdot )}.

Кратные произведения aa{\displaystyle aa}, aaa{\displaystyle aaa}, …{\displaystyle …} записывают в виде натуральных степеней a2{\displaystyle a^{2}}, a3{\displaystyle a^{3}},…{\displaystyle …}^[7]. Для элемента a{\displaystyle a} корректно^[8] определена целая степень, записывается следующим образом: a0=e{\displaystyle a^{0}=e}, a−n=(a−1)n{\displaystyle a^{-n}=(a^{-1})^{n}}.

Аддитивная запись[править | править код]

В коммутативной группе определяющая операция часто рассматривается как (абстрактное) сложение и записывается аддитивно:

Если групповая операция именуется сложением, то саму такую группу G{\displaystyle \mathrm {G} } при этом называют аддитивной и при полном способе записи обозначают так: (G,+){\displaystyle (\mathrm {G} ,+)}^[9].

Существует гигантское количество примеров групп, а также их применений в современном мире. Множество целых чисел, снабжённое операцией сложения, является аддитивной группой или группой по сложению. Множество рациональных чисел, не включающее 0{\displaystyle 0}, с операцией умножения является мультипликативной группой. Эти группы положили начало возникновению важнейших конструкций в разделе общей алгебры. Группы применяются в различных областях математики. Математические объекты часто связываются с группами для дальнейшего изучения их свойств. Например, Анри Пуанкаре основал топологию, введя понятие фундаментальной группы^[10]. Помимо теоретического применения групп существует множество способов применения групп на практике. К примеру, они применяются в криптографии, которая опирается на вычислительную теорию групп и знания в области алгоритмов.

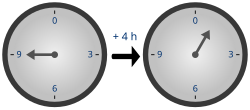Часы показывают время по модулю 12. n=129+4≡1(mod12){\displaystyle {\begin{aligned}n=12\\9+4&\equiv 1{\pmod {12}}\,\end{aligned}}}.

В модульной арифметике складывают два целых числа, а полученную сумму делят на целое положительное число, называемое впоследствии модулем. Результатом модульной операции является остаток от деления. Для любого модуля n{\displaystyle n} множество целых чисел от 0{\displaystyle 0} до n−1{\displaystyle n-1} образует группу по сложению. Обратным элементом к a{\displaystyle a} является число a−1=n−a{\displaystyle a^{-1}=n-a}, нейтральный элемент — 0{\displaystyle 0}. Наглядным примером такой группы могут быть часы с циферблатом^[11].

Применение теории групп не ограничивается только математикой, её широко используют в таких науках как физика, химия и информатика.

• Целые числа с операцией сложения. (Z,+){\displaystyle (\mathbb {Z} ,+)} — коммутативная группа с нейтральным элементом 0{\displaystyle 0}. Целые числа с операцией умножения не будут образовывать группу. Замкнутость, ассоциативность и существование нейтрального элемента будет иметь место, но не выполнится аксиома о существовании обратного элемента. Например, a=2{\displaystyle a=2}, тогда a⋅b=1{\displaystyle a\cdot b=1} то есть b=1/2{\displaystyle b=1/2}. Обратный элемент не является целым числом^[12].
• Положительные рациональные числа с операцией умножения. Произведение рациональных чисел — снова рациональное число, обратный элемент к рациональному числу представляется обратной дробью, имеется ассоциативность, а нейтральным элементом является единица^[12].
• Свободная группа с двумя образующими (F2{\displaystyle F_{2}}) состоит из пустого слова (единица группы) и всех конечных слов из четырёх символов a{\displaystyle a}, a−1{\displaystyle a^{-1}}, b{\displaystyle b} и b−1{\displaystyle b^{-1}} таких, что a{\displaystyle a} не появляется рядом с a−1{\displaystyle a^{-1}} и b{\displaystyle b} не появляется рядом с b−1{\displaystyle b^{-1}}. Операция умножения таких слов — это просто соединение двух слов в одно с последующим сокращением пар aa−1{\displaystyle aa^{-1}}, a−1a{\displaystyle a^{-1}a}, bb−1{\displaystyle bb^{-1}} и b−1b{\displaystyle b^{-1}b}^[13].
• Симметрическая группа. Множество всех биекций конечного множества в себя с операцией композиции является конечной группой, которая называется симметрической группой, или группой перестановок. Мощность конечной симметрической группы Sn{\displaystyle S_{n}} для множества из n{\displaystyle n} элементов равна n!{\displaystyle n!}. При n≥3{\displaystyle n\geq 3} эта группа не является абелевой^[14]. Любая конечная группа является подгруппой некоторой симметрической группы (теорема Кэли)^[12][15].

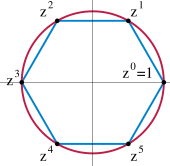6 комплексных корней из единицы образуют циклическую группу

31≡3(mod5)32≡4(mod5)33≡2(mod5)34≡1(mod5){\displaystyle {\begin{aligned}3^{1}&\equiv 3{\pmod {5}}\\3^{2}&\equiv 4{\pmod {5}}\\3^{3}&\equiv 2{\pmod {5}}\\3^{4}&\equiv 1{\pmod {5}}\,\end{aligned}}}

• Группа кубика Рубика — подгруппа симметрической группы S48{\displaystyle S_{48}}, элементы которой соответствуют преобразованиям кубика Рубика. Композиция двух преобразований снова является преобразованием, для каждого преобразования существует обратный элемент, имеется ассоциативность и нейтральный элемент^[17].
• Группы Галуа. Были введены в математику для решения полиномиальных уравнений с помощью свойств симметрии. Например, решение квадратного уравнения ax2+bx+c=0{\displaystyle ax^{2}+bx+c=0} даёт корни: x=−b±b2−4ac2a.{\displaystyle x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}.} Подобная формула есть для уравнения третьей и четвёртой степени, но не существует для полиномиального уравнения степени 5{\displaystyle 5} и выше^[18].

• Для каждого элемента a{\displaystyle a} обратный элемент a−1{\displaystyle a^{-1}} единственен.
• Нейтральный элемент единственен:

  Если e1,e2{\displaystyle e_{1},e_{2}}— нейтральные, то e1⋅e2=e1=

Какая группа крови самая востребованная в донорстве – классификация групп, и что такое резус-фактор

Переливание крови – это распространенный и эффективный метод лечения. Если данной биологической жидкости в организме мало, или она приобрела патологические свойства, может наступить смерть. Поэтому для спасения жизни и борьбы с серьезными заболеваниями нужны доноры. Благодаря переливанию крови врачи успешно спасают жизнь тысячам людей. Гемотрансфузию применяют с середины позапрошлого века.

Гемотрансфузия – это процедура, к проведению которой врачи должны тщательно подготовиться, чтобы не навредить пациенту. Если кровь донора и реципиента несовместима, это приведет к серьезным проблемам и даже к смерти.

Если смешать разные группы, происходит реакция агглютинации, когда эритроциты слипаются между собой и больше не выполняют свои функции, или же в организме реципиента выделяются антитела и разрушают чужеродные клетки.

Для классификации крови применяют систему АВ0 (по группам). Согласно ей, есть только четыре группы: первая – 0, вторая обозначается латинской буквой А, третья – В и четвертая, ее помечают двумя буквами – АВ.

По резус-фактору есть только два вида: положительная и отрицательная. Исходя из этого, выделяется 8 комбинаций типов крови. Часто возникает вопрос, какая группа крови самая востребованная в донорстве?

Сразу же стоит прояснить, что есть универсальная кровь, которая подходит всем, ее безопасно переливать любому человеку. Она распространена, поэтому не считается самой востребованной в донорстве. И есть кровь, носителей которой очень мало на Земле, она считается редкой.

Группа крови и резус-фактор, рассмотрим подробнее

Что значат обозначения группы крови и резус фактора? Комбинация антигенов в эритроцитах и плазме крови определяет группу. Она никогда не меняется у человека, поскольку набор белков в клетках всегда одинаков.

Ученые составили несколько классификаций крови, они появились потому, что на клетках присутствует множество антигенов, которые образуют антигеновые системы. На практике используют только одну АВ0 классификацию.

На красных кровяных тельцах человека есть три вида антигенов: Н – неактивный, А, В и АВ – активные. Этими латинскими буквами зашифровывают группы. Только вместо буквы Н пишут цифру 0 для удобства, что означает, что антигенов нет. Возле буквенного обозначения пишут I, II, III или IV. По этим латинским цифрам люди могут понять, какая же группа крови зашифрована.

Помимо этого, в крови есть особый белок, он называется агглютинином. Его обозначают двумя греческими буквами – бета и альфа. Именно он приводит к разрушению эритроцитов, если те несут не совпадающий набор белков. Это происходит, когда в организм попадает не такая группа крови, как у реципиента.

Исходя из этого понятно, что есть конкретная комбинация антигенов и агглютининов, по которой и определяется группа крови. Вторая группа содержит антиген А и агглютинин бета. В третьей, наоборот, В и альфа. В первой группе есть оба агглютинина, так как антигенов нет. В плазме четвертой группы есть А и В антигены, поэтому нет агглютининов.

Совместимой считается плазма и форменные элементы с одинаковым набором белков. Только тогда она приживется в организме реципиента после переливания.

Кровь человека имеет постоянный резус-фактор, его пишут как Rh, + или в зависимости от того, положительный он или отрицательный. Резус-фактор тоже по присутствию антигенов на поверхности эритроцитов. Белков, которые кодируют резус-фактор, 6. Если на клетках есть белок D, или C+E, то кровь Rh+. Если данных антигенов нет – Rh-.

По этому показателю тоже определяют безопасно делать переливание или нет.  Но если ситуация критичная, допустимо смешать положительный и отрицательный резус.

Какая группа самая распространенная

Какая кровь самая востребованная в медицине для донорства, редкая или распространенная? давайте разберемся.

Опираясь на статистику, отметим, что чаще других встречается первая группа. Примерно половина всего населения планеты ее носитель. С II (A) – 40% населения. Только 9% людей с третей группой, и 4% – с четвертой. У подавляющего большинства (85%) – Rh+. И только у 15% – резус-отрицательный фактор.

Делаем вывод, что людей с I(0) Rh+ кровью больше всех, поэтому она и самая распространенная. IV (AB) Rh- считается самой редкой. Иногда она очень нужна, поэтому собирается и хранится в специальных банках, где ее можно приобрести. Сколько стоит 4 группа крови, можно узнать в банке или у врача.

Универсальная – значит лучшая?

Есть универсальные доноры – это люди с первой группой. Все потому, что на их эритроцитах нет белков-антигенов, поэтому организм реципиента не воспринимает ее как чужеродную, и не вырабатывает антитела, которые разрушают влитые клетки. Благодаря своей универсальности первая группа считается лучшей.

А группы крови с А и В белками можно вливать только людям с таким же набором. Есть также универсальный реципиент – это человек с четвертой группой. Его организм примет любой набор антигенов.

Однако перечисленные выше правила в практической медицине не применяются. Сегодня запрещено смешивать разные группы и резус-факторы. Поэтому и донор, и реципиент должны иметь одинаковый набор белков. Исключение делают только в экстренных случаях.

И все же, какая группа самая востребованная?

Исходя из приведенной информации,  напрашивается два вывода:

1. Наиболее востребована группа крови I (0) Rh+, так как людей с этой группой подавляющее большинство.
2. IV (АВ) резус-положительной и отрицательной намного меньше, поэтому и найти ее сложнее. Все потому что людей, в жилах которых течет такая кровь, очень мало. И если больному придется делать переливание, найти донора будет сложно.

Можно сказать, что самая востребованная группа крови в донорстве – это четвертая, так как ее меньше всех на планете.

В каких случаях требуется переливать кровь?

Переливание делают из-за сильных кровопотерь. Если пациент теряет около 30% крови в течение нескольких часов, в таком случае нужно проводить данную процедуру. Еще ее неотложно делают, если человек в шоковом состоянии после лечения хирургическими методами.

Нередко переливание назначают пациентам, у которых диагностировали анемию, серьезные заболевания крови, воспалительные процессы в организме и гнойно-септические болезни, сильные и тяжелые интоксикации организма.

Процедуру назначают людям с такими болезнями:

• лейкопения – резкое понижение уровня лейкоцитов,
• гипопротеинемия – низкий уровень белка в крови,
• сепсис – заражение крови микробами,
• нарушение СОЭ.

Для переливания смешивают кровь со всеми ее компонентами, препараты и кровезаменители. В обычную кровь донора добавляют лекарства, которые повышают лечебный эффект, при этом снижается риск возникновения осложнений после процедуры.

Часто в организм больного вводят эритроцитарную массу. Для этого эритроциты сначала отделяют от замороженной плазмы. После этого вливают жидкость с большой концентрацией красных клеток в организм реципиента. Такой метод применяют при анемиях, острых кровопотерях, при развитии злокачественных опухолей, после пересадки тканей и органов.

Массу лейкоцитов вливают при агранулоцитозе, когда уровень этих клеток стремительно снижается, и лечении тяжелых осложнений заболеваний инфекционной природы. После процедуры уровень белых клеток в крови повышается, что благоприятно влияет на протекание выздоровления.

Когда применяют свежезамороженную плазму:

• сильные кровопотери,
• ДВС-синдром,
• геморрагии – кровь вытекает через поврежденные стенки сосудов,
• передозировка коагулянтов,
• болезни инфекционной природы.

Особенно нуждаются в переливании пациенты с заболеваниями крови. Некоторым больным приходится раз в неделю, а то и чаще делать такую процедуру.

Делают переливание и людям после химиотерапии. Если опухоль поразила костный мозг, после терапии прекращают расти не только злокачественные клетки, но и здоровые.

Часто переливание нужно женщинам после сложных родов, во время которых они потеряли много крови. Иногда врачи не рекомендуют использовать для этого кровь мужчины. Женская считается безопаснее, а для молодой мамы это особенно важно.

Противопоказания

Это сложная и рискованная процедура. В случае неудачи произойдет ряд нарушений жизненно важных процессов в организме. Поэтому врачи всегда серьезно подходят к этому вопросу. Исследуют заболевания и информацию о переливаниях, которые уже делали больному.

Процедура противопоказана больным с пороками и другими серьезными заболеваниями сердца. При нарушениях кровотока в сосудах головного мозга и белкового обмена в организме, при аллергии.

Часто даже при наличии противопоказаний и серьезных заболеваний, для лечения которых требуется переливание, врачи проводят эту процедуру. Но при этом они назначают пациенту препараты для профилактики болезней, которые могут проявиться после нее.

Поэтому на вопрос, какая группа крови наиболее востребована в современном донорстве, ответ неоднозначный. Так как реципиенту переливают только родную группу, а людей с I (0) Rh+ больше всех, и переливание им делают чаще, то она востребованная. А людей с IV (АВ) Rh+ или намного меньше, но если человеку с такой группой нужно будет делать переливание, найти донора проблематично.

Загрузка…

Как распределяют детей по группам в детских садиках

При выборе детского сада возникает множество вопросов, например, о группах в детском садике, их видах, количестве, а также, куда будет распределен ребенок.

Родителей волнует вопрос распределения ребенка в по возрастным категориям. Поэтому их интересует, какие группы имеются в детском саду, подразделяется ли младшая группа на первую и вторую, или же она единственная?

Как правило, в первую младшую группу распределяют детей от 1,5 до 3 лет. Во вторую младшую принимают детей от 3 лет. Если в садике, который вы выбрали, принимают детей только с двух лет, тогда младшая группа одна в садике, без подразделений.

Принято считать, что обычный садик включает четыре группы: ясельную, младшую, среднюю группу и старшую. Но есть сады, где эти группы разделяются еще на дополнительные младшие группы, о которых было сказано выше, подготовительные группы, где упор делается на подготовку детей к школе. Бывают логопедические группы, но они, как правило, есть в специализированных садиках. Такие группы предназначены для коррекции определенных функций ребенка. Если в садике такие подразделения имеются, то он обязан иметь в штате первоклассных специалистов своего дела, что, к сожалению, не везде встречается.

Сегодня в большинстве садиках сделано оптимальное разделение детей по возрастным группам. Формируются группы:

1. ясельная – дети от 1,5 до 2 лет;

2. первая младшая – 2-3 года;

3. вторая младшая – 3-4 года;

4. средняя – 4-5 лет;

5. старшая – 5-6 лет;

6. подготовительная – 6-7 лет.

Распределение детей по данным категориям необходимо для удобства ведения статистики, а, главное, для повышения качества образовательного процесса, так как дети из близкой категории возраста в одном коллективе легче усваивают умения и навыки.

Данная группа является дополнительным видом групп в детском саду. Сегодня уже можно услышать о такой группе. Это, конечно, роскошь, которая доступна в основном лишь в частных детских садах и садиках элитной категории.

Группы для неполного пребывания в детском саду нужны тем мамам, которые по каким-либо причинам не готовы определить ребенка в детский сад на полный день. Кроме этого, такие группы обычно комплектуются всего лишь из 10-12 детей, что добавляет родителям удобства и уверенности.

Чем отличается группа от сообщества Вконтакте

Вопрос о том, чем отличается группа от сообщества ВКонтакте, волнует многих пользователей социальной сети. Каждый юзер в ВК может создать сообщество для общения, распространения информации или продвижения товаров и услуг. В процессе создания социальная сеть просит определить тип будущей страницы. Это может быть мероприятие, группа или публичная страница. Если с первым видом всё более-менее понятно (сообщество Мероприятие служит для организации семинара, тренинга, концерта и приглашения на него максимального числа участников), то вокруг группы и публичной страницы сосредоточено немало вопросов.

Для каких ситуаций подходит то или иное сообщество? Какими преимуществами они обладают? И как правильно выбрать тип? Подробно рассмотрим эти вопросы в данной статье.

Что такое Группа и Публичная страница ВКонтакте

Публичная страница, которую в просторечье часто называют Паблик, представляет собой официальную страничку для распространения информации о продукте, услуге, личности, бренде, компании. Кроме того, публичная страница может быть посвящена какому-то тематическому сегменту: прически и макияж, автомобили и мотоциклы, детское развитие и т. д. Источником информации здесь выступает создатель или администратор сообщества. Он же может включить или отключить возможность для комментирования подписчиками.

Под Группой понимают сообщество, где юзеры объединены по интересам и могут свободно обмениваться информацией. При этом группы могут быть открытыми, закрытыми или частными, что позволяет настраивать сообщество под потребности целевой аудитории.

Преимущества и недостатки групп и публичных страниц

Группы и паблики обладают собственными преимуществами и недостатками, которые в результате и определяют выбор сообщества в конкретной ситуации.

Плюсы и минусы публичной страницы ВК

• Контент в паблике полностью открыт для всех пользователей социальной сети.
• Право на размещение постов есть только у владельца и администратора. Подписчики могут лишь предложить новость или комментировать имеющиеся записи, если это позволяют настройки страницы.
• Альбомы с фотографиями, видеоролики и обсуждения располагаются в правой части экрана.
• В рамках публичной страницы можно создать мероприятие.
• Раздел со свежими новостями отсутствует, однако можно добавить wiki-страницу.
• Публичная страница не подходит для хранения файлов и документов.
• Отсутствует опция приглашения друзей.
• На каждой личной страничке юзера ВК имеется блок Интересные страницы. Логотип публичной страницы в данном блоке обеспечивает дополнительный трафик подписчиков.

Плюсы и минусы группы ВК

• Существует три типа группы: открытая (контент доступен для всех пользователей), закрытая (добавление в группу осуществляется по пользовательской заявке), частная (вступление в группу возможно только по приглашению администратора).
• В группе с открытой стеной пользователи могут сами размещать посты. Однако имеется возможность закрыть стену. Тогда добавлением записей занимается только администратор.
• Аудиозаписи, видеоролики и фотографии находятся под новостями в верхней части экрана.
• Группа не подходит для создания мероприятий.
• В соответствующем разделе группы можно публиковать свежие новости.
• В разделе Документы можно хранить файлы, важные для функционирования сообщества, в том числе текстовые документы и таблицы.
• Имеется специальная функция для приглашения в группу друзей. При этом, воспользоваться ею может не только администратор, но и любой участник. Это способствует быстрому продвижению и наращиванию трафика в сообществе.
• Несмотря на то, что на каждой личной страничке имеется блок с группами, даже наличие в нем логотипа группы не обеспечивает повышенного внимания других пользователей.

Отличия в продвижении группы и публичной страницы

Остается рассмотреть вопрос о том, что лучше для продажи товаров и услуг в сети. Администраторы групп могут воспользоваться кнопкой Пригласить друзей, это весьма облегчает раскрутку сообщества. Публичные страницы лишены такой возможности.

Внимание! В сутки один человек может отправить не более 40 приглашений. Такие ограничения были введены со стороны социальной сети и действуют для всех пользователей без исключений. Чтобы эффективно использовать этот инструмент, специалисты рекомендуют работать с нескольких аккаунтов.

Главным преимуществом публичной страницы для продвижения является ее видимость на личных страничках подписчиков. Логотип с названием и описанием в разделе Интересные страницы — прекрасная ненавязчивая реклама для каждого сообщества.

В свою очередь, название группы помещается в неструктурированный список под личной информацией пользователя. Как правило, на этот блок никто не обращает внимания, и тем более не интересуется им специально. К тому же, в настройках страницы есть возможность для сокрытия данного блока.

Теперь коснемся пользовательской активности. Очевидно, что она выше на публичных страницах, так как данный формат прямо направлен на взаимопиар и продвижение. Достичь столь же высокого уровня активности в группе также возможно, но для этого придется приложить немало усилий.

Необходимо отметить и то, что в данный момент среди юзеров в ВК сложился стереотип об устаревании групп. Считаются, что группы уже выходят из моды, а на смену им приходят публичные страницы. В связи с этим, пользователи часто подписываются на паблики, избегая участия в группах.

Таким образом, между группой и публичной страничкой в ВКонтакте имеется немало различий. Они касаются как структуры, так и функционала сообществ. Эти различия объясняют и разность в стратегиях продвижения и монетизации. Однако конечный результат в любом случае зависит от профессионализма и опыта администратора, его терпения и настойчивости, временных и финансовых ресурсов.